A neural operator-based surrogate solver for free-form electromagnetic inverse design

Neural operators have emerged as a powerful tool for solving partial differential equations in the context of scientific machine learning. Here, we implement and train a modified Fourier neural operator as a surrogate solver for electromagnetic scattering problems and compare its data efficiency to existing methods. We further demonstrate its application to the gradient-based nanophotonic inverse design of free-form, fully three-dimensional electromagnetic scatterers, an area that has so far eluded the application of deep learning techniques.

Bayesian optimization with improved scalability and derivative information for efficient design of nanophotonic structures

We propose the combination of forward shape derivatives and the use of an iterative inversion scheme for Bayesian optimization to find optimal designs of nanophotonic devices. This approach widens the range of applicability of Bayesian optmization to situations where a larger number of iterations is required and where derivative information is available. This was previously impractical because the computational efforts required to identify the next evaluation point in the parameter space became much larger than the actual evaluation of the objective function. We demonstrate an implementation of the method by optimizing a waveguide edge coupler.

Benchmarking five global optimization approaches for nano-optical shape optimization and parameter reconstruction

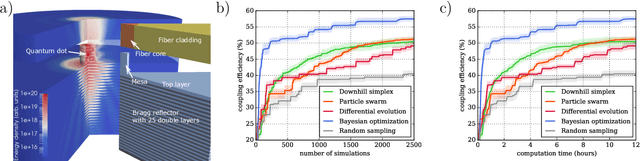
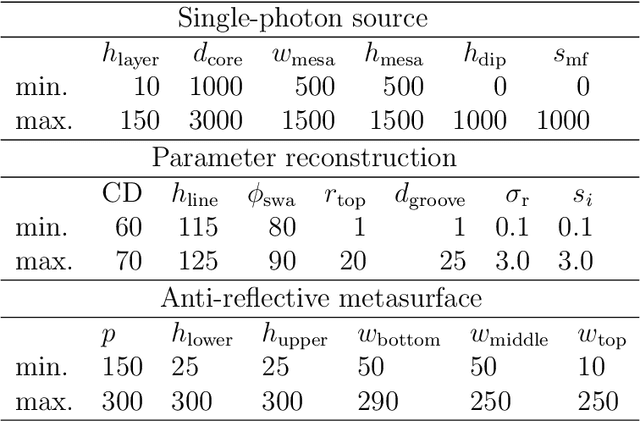
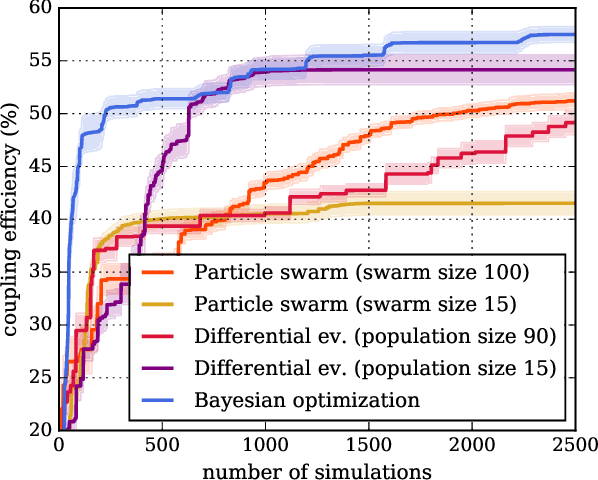
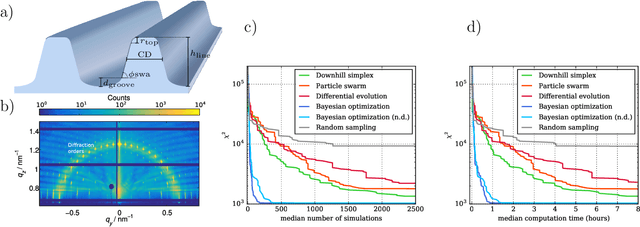
Numerical optimization is an important tool in the field of computational physics in general and in nano-optics in specific. It has attracted attention with the increase in complexity of structures that can be realized with nowadays nano-fabrication technologies for which a rational design is no longer feasible. Also, numerical resources are available to enable the computational photonic material design and to identify structures that meet predefined optical properties for specific applications. However, the optimization objective function is in general non-convex and its computation remains resource demanding such that the right choice for the optimization method is crucial to obtain excellent results. Here, we benchmark five global optimization methods for three typical nano-optical optimization problems from the field of shape optimization and parameter reconstruction: downhill simplex optimization, the limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) algorithm, particle swarm optimization, differential evolution, and Bayesian optimization. In these examples, Bayesian optimization, mainly known from machine learning applications, obtains significantly better results in a fraction of the run times of the other optimization methods.