Marek Grześ
Can Large Language Models Outperform Non-Experts in Poetry Evaluation? A Comparative Study Using the Consensual Assessment Technique
Feb 26, 2025Abstract:The Consensual Assessment Technique (CAT) evaluates creativity through holistic expert judgments. We investigate the use of two advanced Large Language Models (LLMs), Claude-3-Opus and GPT-4o, to evaluate poetry by a methodology inspired by the CAT. Using a dataset of 90 poems, we found that these LLMs can surpass the results achieved by non-expert human judges at matching a ground truth based on publication venue, particularly when assessing smaller subsets of poems. Claude-3-Opus exhibited slightly superior performance than GPT-4o. We show that LLMs are viable tools for accurately assessing poetry, paving the way for their broader application into other creative domains.
Structure learning with Temporal Gaussian Mixture for model-based Reinforcement Learning
Nov 18, 2024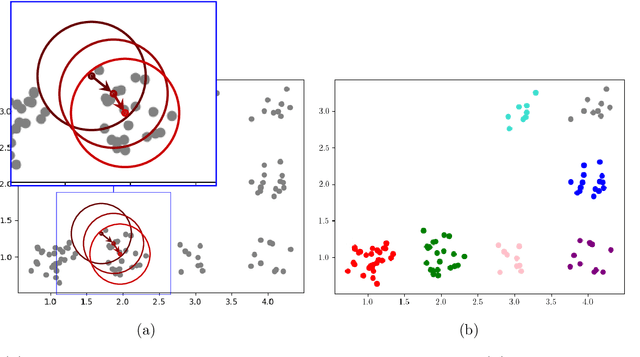
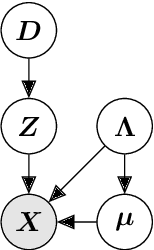
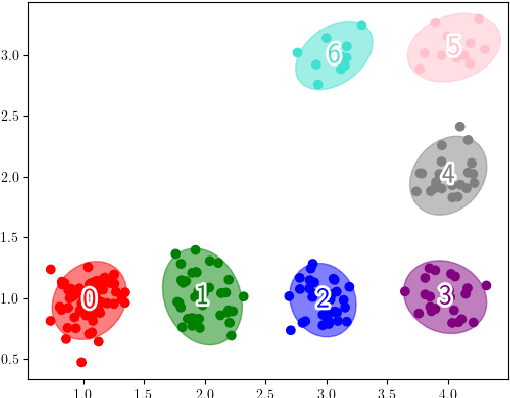
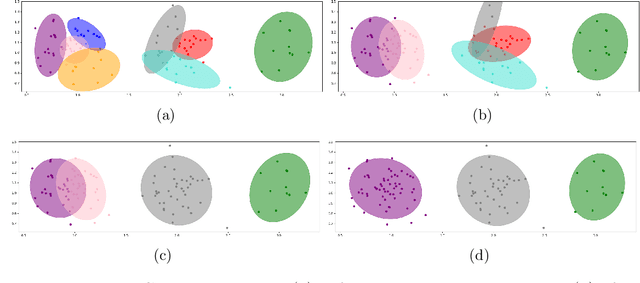
Abstract:Model-based reinforcement learning refers to a set of approaches capable of sample-efficient decision making, which create an explicit model of the environment. This model can subsequently be used for learning optimal policies. In this paper, we propose a temporal Gaussian Mixture Model composed of a perception model and a transition model. The perception model extracts discrete (latent) states from continuous observations using a variational Gaussian mixture likelihood. Importantly, our model constantly monitors the collected data searching for new Gaussian components, i.e., the perception model performs a form of structure learning (Smith et al., 2020; Friston et al., 2018; Neacsu et al., 2022) as it learns the number of Gaussian components in the mixture. Additionally, the transition model learns the temporal transition between consecutive time steps by taking advantage of the Dirichlet-categorical conjugacy. Both the perception and transition models are able to forget part of the data points, while integrating the information they provide within the prior, which ensure fast variational inference. Finally, decision making is performed with a variant of Q-learning which is able to learn Q-values from beliefs over states. Empirically, we have demonstrated the model's ability to learn the structure of several mazes: the model discovered the number of states and the transition probabilities between these states. Moreover, using its learned Q-values, the agent was able to successfully navigate from the starting position to the maze's exit.
Reframing the Expected Free Energy: Four Formulations and a Unification
Feb 22, 2024Abstract:Active inference is a leading theory of perception, learning and decision making, which can be applied to neuroscience, robotics, psychology, and machine learning. Active inference is based on the expected free energy, which is mostly justified by the intuitive plausibility of its formulations, e.g., the risk plus ambiguity and information gain / pragmatic value formulations. This paper seek to formalize the problem of deriving these formulations from a single root expected free energy definition, i.e., the unification problem. Then, we study two settings, each one having its own root expected free energy definition. In the first setting, no justification for the expected free energy has been proposed to date, but all the formulations can be recovered from it. However, in this setting, the agent cannot have arbitrary prior preferences over observations. Indeed, only a limited class of prior preferences over observations is compatible with the likelihood mapping of the generative model. In the second setting, a justification of the root expected free energy definition is known, but this setting only accounts for two formulations, i.e., the risk over states plus ambiguity and entropy plus expected energy formulations.
Deconstructing deep active inference
Mar 02, 2023Abstract:Active inference is a theory of perception, learning and decision making, which can be applied to neuroscience, robotics, and machine learning. Recently, reasearch has been taking place to scale up this framework using Monte-Carlo tree search and deep learning. The goal of this activity is to solve more complicated tasks using deep active inference. First, we review the existing literature, then, we progresively build a deep active inference agent. For two agents, we have experimented with five definitions of the expected free energy and three different action selection strategies. According to our experiments, the models able to solve the dSprites environment are the ones that maximise rewards. Finally, we compare the similarity of the representation learned by the layers of various agents using centered kernel alignment. Importantly, the agent maximising reward and the agent minimising expected free energy learn very similar representations except for the last layer of the critic network (reflecting the difference in learning objective), and the variance layers of the transition and encoder networks. We found that the reward maximising agent is a lot more certain than the agent minimising expected free energy. This is because the agent minimising expected free energy always picks the action down, and does not gather enough data for the other actions. In contrast, the agent maximising reward, keeps on selecting the actions left and right, enabling it to successfully solve the task. The only difference between those two agents is the epistemic value, which aims to make the outputs of the transition and encoder networks as close as possible. Thus, the agent minimising expected free energy picks a single action (down), and becomes an expert at predicting the future when selecting this action. This makes the KL divergence between the output of the transition and encoder networks small.
Multi-Modal and Multi-Factor Branching Time Active Inference
Jun 24, 2022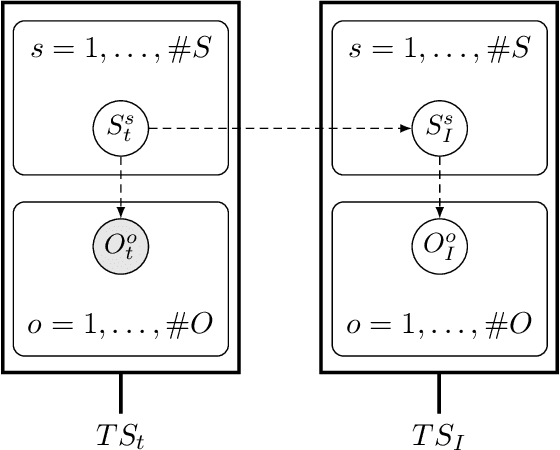
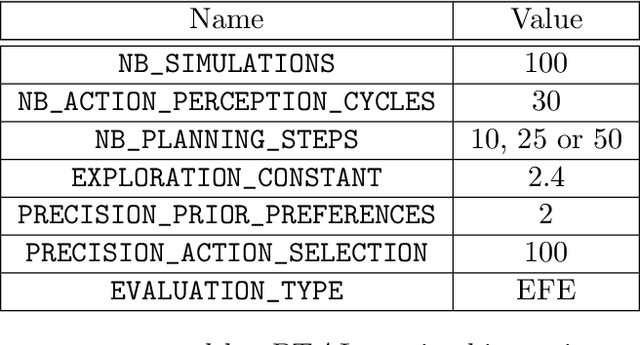

Abstract:Active inference is a state-of-the-art framework for modelling the brain that explains a wide range of mechanisms such as habit formation, dopaminergic discharge and curiosity. Recently, two versions of branching time active inference (BTAI) based on Monte-Carlo tree search have been developed to handle the exponential (space and time) complexity class that occurs when computing the prior over all possible policies up to the time horizon. However, those two versions of BTAI still suffer from an exponential complexity class w.r.t the number of observed and latent variables being modelled. In the present paper, we resolve this limitation by first allowing the modelling of several observations, each of them having its own likelihood mapping. Similarly, we allow each latent state to have its own transition mapping. The inference algorithm then exploits the factorisation of the likelihood and transition mappings to accelerate the computation of the posterior. Those two optimisations were tested on the dSprites environment in which the metadata of the dSprites dataset was used as input to the model instead of the dSprites images. On this task, $BTAI_{VMP}$ (Champion et al., 2022b,a) was able to solve 96.9\% of the task in 5.1 seconds, and $BTAI_{BF}$ (Champion et al., 2021a) was able to solve 98.6\% of the task in 17.5 seconds. Our new approach ($BTAI_{3MF}$) outperformed both of its predecessors by solving the task completly (100\%) in only 2.559 seconds. Finally, $BTAI_{3MF}$ has been implemented in a flexible and easy to use (python) package, and we developed a graphical user interface to enable the inspection of the model's beliefs, planning process and behaviour.
Branching Time Active Inference with Bayesian Filtering
Dec 14, 2021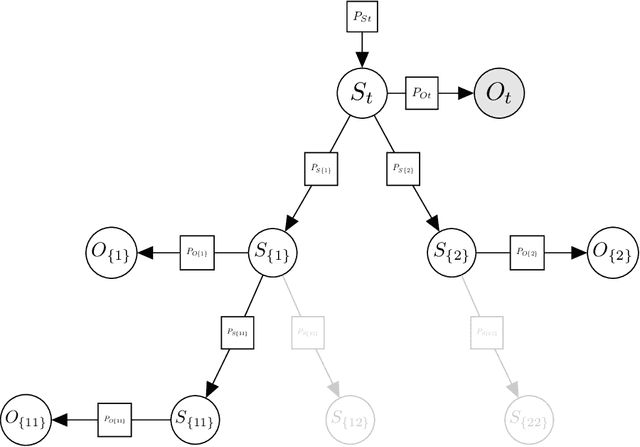
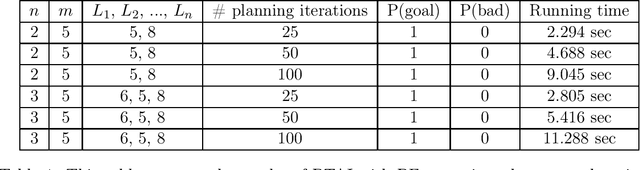
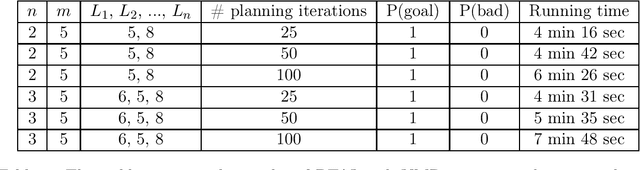
Abstract:Branching Time Active Inference (Champion et al., 2021b,a) is a framework proposing to look at planning as a form of Bayesian model expansion. Its root can be found in Active Inference (Friston et al., 2016; Da Costa et al., 2020; Champion et al., 2021c), a neuroscientific framework widely used for brain modelling, as well as in Monte Carlo Tree Search (Browne et al., 2012), a method broadly applied in the Reinforcement Learning literature. Up to now, the inference of the latent variables was carried out by taking advantage of the flexibility offered by Variational Message Passing (Winn and Bishop, 2005), an iterative process that can be understood as sending messages along the edges of a factor graph (Forney, 2001). In this paper, we harness the efficiency of an alternative method for inference called Bayesian Filtering (Fox et al., 2003), which does not require the iteration of the update equations until convergence of the Variational Free Energy. Instead, this scheme alternates between two phases: integration of evidence and prediction of future states. Both of those phases can be performed efficiently and this provides a seventy times speed up over the state-of-the-art.
Branching Time Active Inference: empirical study and complexity class analysis
Nov 22, 2021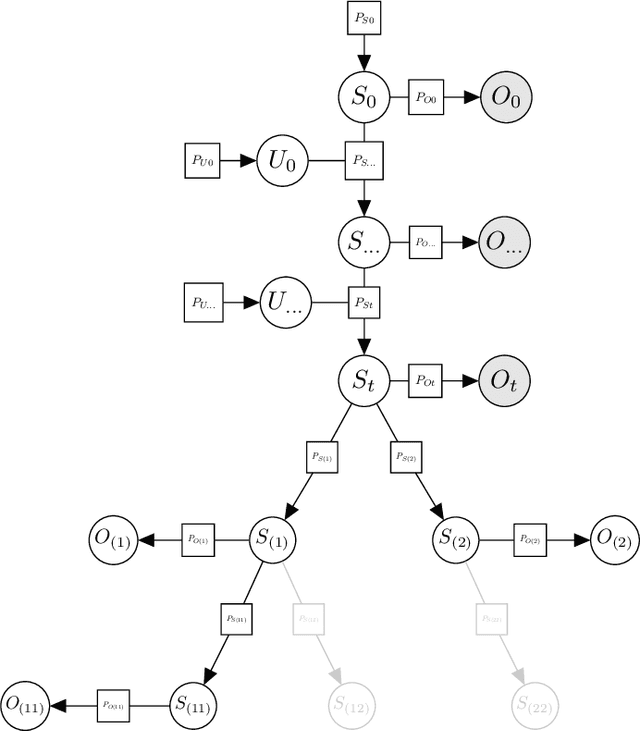
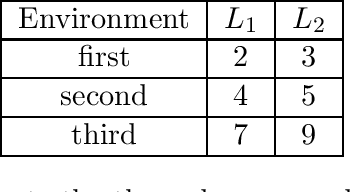
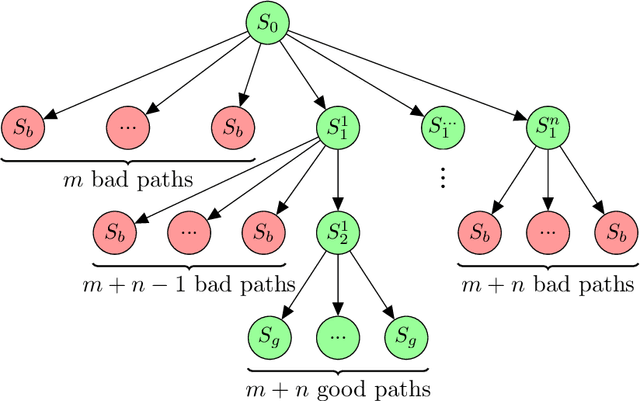

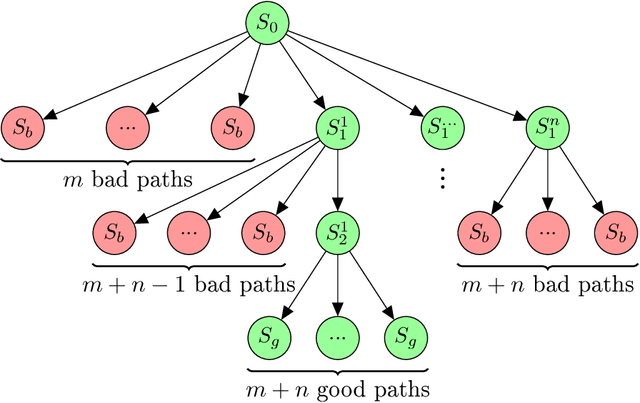
Abstract:Active inference is a state-of-the-art framework for modelling the brain that explains a wide range of mechanisms such as habit formation, dopaminergic discharge and curiosity. However, recent implementations suffer from an exponential (space and time) complexity class when computing the prior over all the possible policies up to the time horizon. Fountas et al. (2020) used Monte Carlo tree search to address this problem, leading to very good results in two different tasks. Additionally, Champion et al. (2021a) proposed a tree search approach based on structure learning. This was enabled by the development of a variational message passing approach to active inference (Champion et al., 2021b), which enables compositional construction of Bayesian networks for active inference. However, this message passing tree search approach, which we call branching-time active inference (BTAI), has never been tested empirically. In this paper, we present an experimental study of the approach (Champion et al., 2021a) in the context of a maze solving agent. In this context, we show that both improved prior preferences and deeper search help mitigate the vulnerability to local minima. Then, we compare BTAI to standard active inference (AI) on a graph navigation task. We show that for small graphs, both BTAI and AI successfully solve the task. For larger graphs, AI exhibits an exponential (space) complexity class, making the approach intractable. However, BTAI explores the space of policies more efficiently, successfully scaling to larger graphs.
Branching Time Active Inference: the theory and its generality
Nov 22, 2021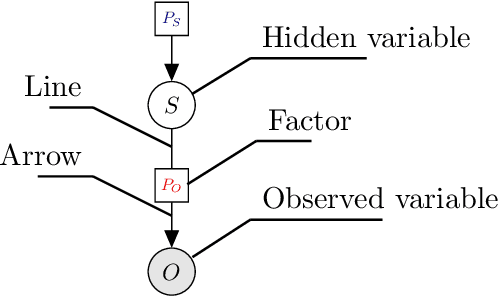

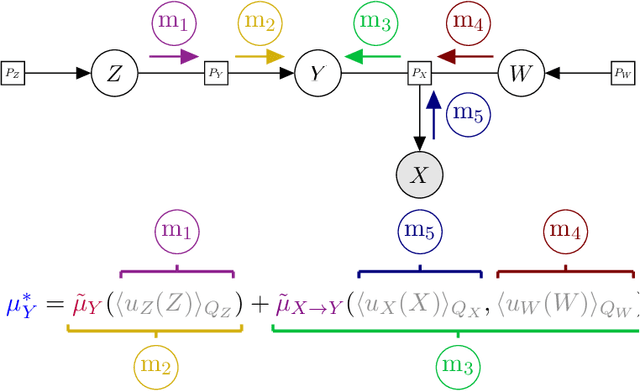
Abstract:Over the last 10 to 15 years, active inference has helped to explain various brain mechanisms from habit formation to dopaminergic discharge and even modelling curiosity. However, the current implementations suffer from an exponential (space and time) complexity class when computing the prior over all the possible policies up to the time-horizon. Fountas et al (2020) used Monte Carlo tree search to address this problem, leading to impressive results in two different tasks. In this paper, we present an alternative framework that aims to unify tree search and active inference by casting planning as a structure learning problem. Two tree search algorithms are then presented. The first propagates the expected free energy forward in time (i.e., towards the leaves), while the second propagates it backward (i.e., towards the root). Then, we demonstrate that forward and backward propagations are related to active inference and sophisticated inference, respectively, thereby clarifying the differences between those two planning strategies.
Realising Active Inference in Variational Message Passing: the Outcome-blind Certainty Seeker
Apr 23, 2021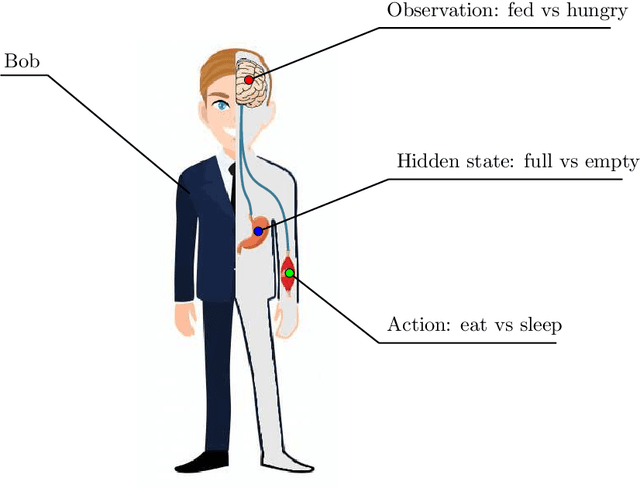
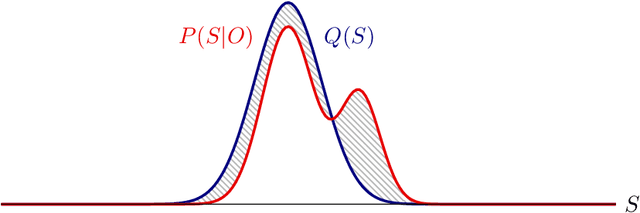

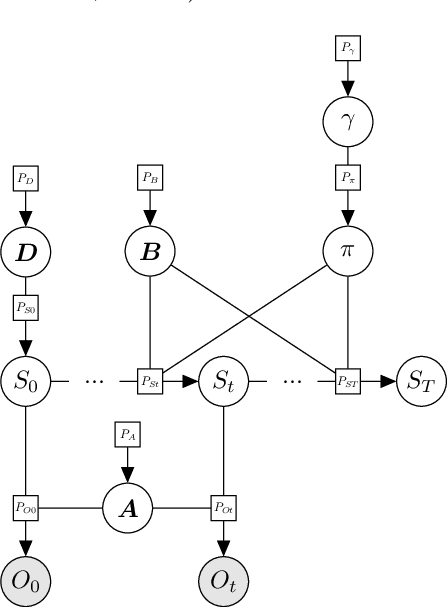
Abstract:Active inference is a state-of-the-art framework in neuroscience that offers a unified theory of brain function. It is also proposed as a framework for planning in AI. Unfortunately, the complex mathematics required to create new models -- can impede application of active inference in neuroscience and AI research. This paper addresses this problem by providing a complete mathematical treatment of the active inference framework -- in discrete time and state spaces -- and the derivation of the update equations for any new model. We leverage the theoretical connection between active inference and variational message passing as describe by John Winn and Christopher M. Bishop in 2005. Since, variational message passing is a well-defined methodology for deriving Bayesian belief update equations, this paper opens the door to advanced generative models for active inference. We show that using a fully factorized variational distribution simplifies the expected free energy -- that furnishes priors over policies -- so that agents seek unambiguous states. Finally, we consider future extensions that support deep tree searches for sequential policy optimisation -- based upon structure learning and belief propagation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge