Realising Active Inference in Variational Message Passing: the Outcome-blind Certainty Seeker
Paper and Code
Apr 23, 2021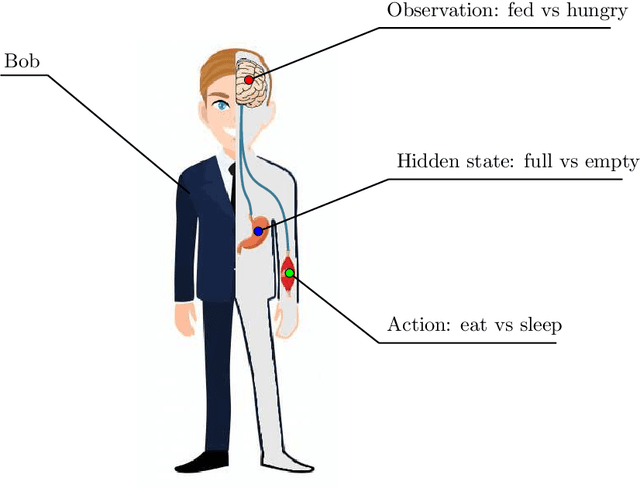
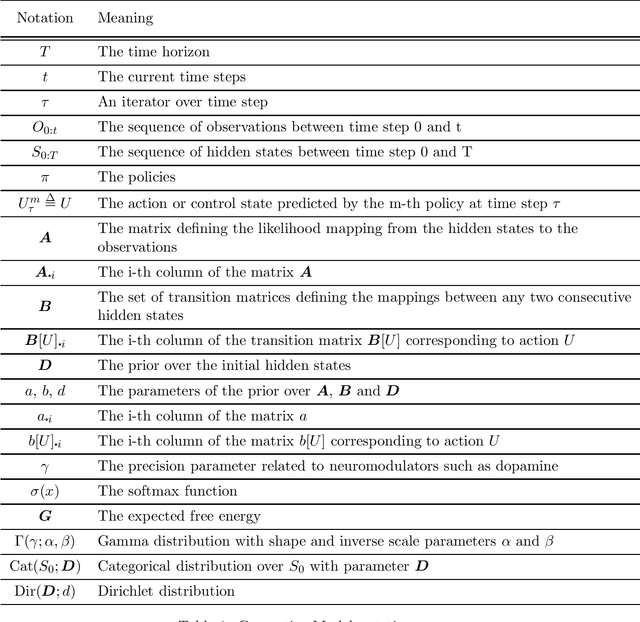
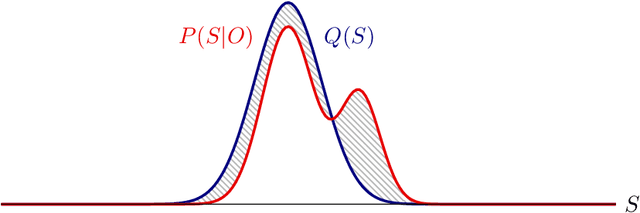

Active inference is a state-of-the-art framework in neuroscience that offers a unified theory of brain function. It is also proposed as a framework for planning in AI. Unfortunately, the complex mathematics required to create new models -- can impede application of active inference in neuroscience and AI research. This paper addresses this problem by providing a complete mathematical treatment of the active inference framework -- in discrete time and state spaces -- and the derivation of the update equations for any new model. We leverage the theoretical connection between active inference and variational message passing as describe by John Winn and Christopher M. Bishop in 2005. Since, variational message passing is a well-defined methodology for deriving Bayesian belief update equations, this paper opens the door to advanced generative models for active inference. We show that using a fully factorized variational distribution simplifies the expected free energy -- that furnishes priors over policies -- so that agents seek unambiguous states. Finally, we consider future extensions that support deep tree searches for sequential policy optimisation -- based upon structure learning and belief propagation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge