Structure learning with Temporal Gaussian Mixture for model-based Reinforcement Learning

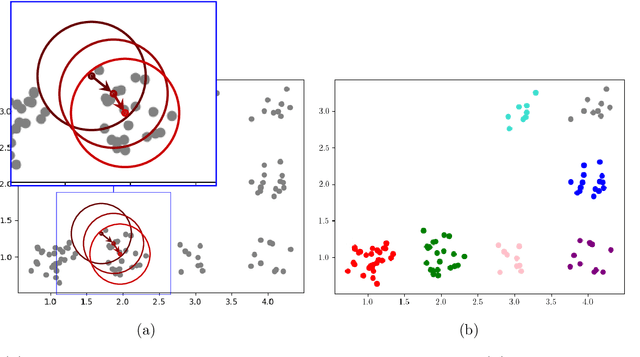
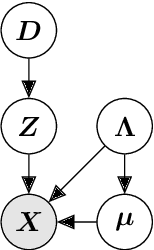
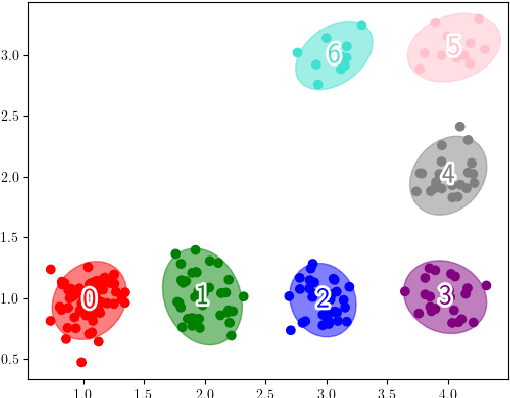
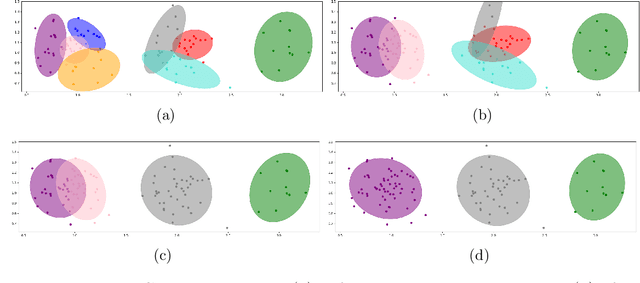
Model-based reinforcement learning refers to a set of approaches capable of sample-efficient decision making, which create an explicit model of the environment. This model can subsequently be used for learning optimal policies. In this paper, we propose a temporal Gaussian Mixture Model composed of a perception model and a transition model. The perception model extracts discrete (latent) states from continuous observations using a variational Gaussian mixture likelihood. Importantly, our model constantly monitors the collected data searching for new Gaussian components, i.e., the perception model performs a form of structure learning (Smith et al., 2020; Friston et al., 2018; Neacsu et al., 2022) as it learns the number of Gaussian components in the mixture. Additionally, the transition model learns the temporal transition between consecutive time steps by taking advantage of the Dirichlet-categorical conjugacy. Both the perception and transition models are able to forget part of the data points, while integrating the information they provide within the prior, which ensure fast variational inference. Finally, decision making is performed with a variant of Q-learning which is able to learn Q-values from beliefs over states. Empirically, we have demonstrated the model's ability to learn the structure of several mazes: the model discovered the number of states and the transition probabilities between these states. Moreover, using its learned Q-values, the agent was able to successfully navigate from the starting position to the maze's exit.