Dominic Zhao
Active Inference as a Model of Agency
Jan 23, 2024



Abstract:Is there a canonical way to think of agency beyond reward maximisation? In this paper, we show that any type of behaviour complying with physically sound assumptions about how macroscopic biological agents interact with the world canonically integrates exploration and exploitation in the sense of minimising risk and ambiguity about states of the world. This description, known as active inference, refines the free energy principle, a popular descriptive framework for action and perception originating in neuroscience. Active inference provides a normative Bayesian framework to simulate and model agency that is widely used in behavioural neuroscience, reinforcement learning (RL) and robotics. The usefulness of active inference for RL is three-fold. \emph{a}) Active inference provides a principled solution to the exploration-exploitation dilemma that usefully simulates biological agency. \emph{b}) It provides an explainable recipe to simulate behaviour, whence behaviour follows as an explainable mixture of exploration and exploitation under a generative world model, and all differences in behaviour are explicit in differences in world model. \emph{c}) This framework is universal in the sense that it is theoretically possible to rewrite any RL algorithm conforming to the descriptive assumptions of active inference as an active inference algorithm. Thus, active inference can be used as a tool to uncover and compare the commitments and assumptions of more specific models of agency.
Learning where to learn: Gradient sparsity in meta and continual learning
Oct 27, 2021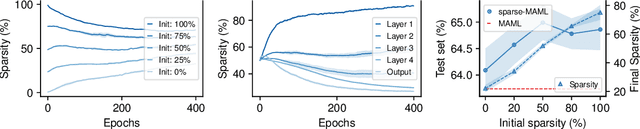
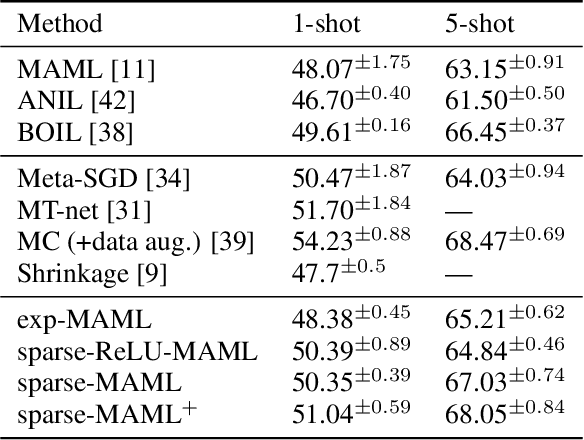
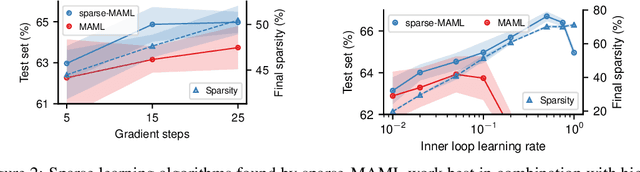
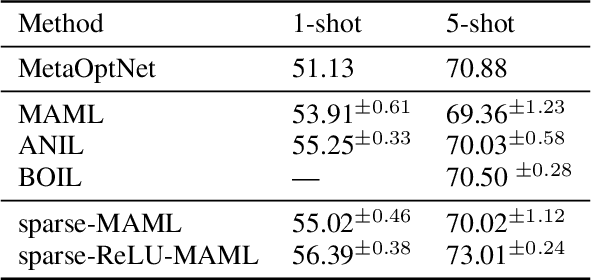
Abstract:Finding neural network weights that generalize well from small datasets is difficult. A promising approach is to learn a weight initialization such that a small number of weight changes results in low generalization error. We show that this form of meta-learning can be improved by letting the learning algorithm decide which weights to change, i.e., by learning where to learn. We find that patterned sparsity emerges from this process, with the pattern of sparsity varying on a problem-by-problem basis. This selective sparsity results in better generalization and less interference in a range of few-shot and continual learning problems. Moreover, we find that sparse learning also emerges in a more expressive model where learning rates are meta-learned. Our results shed light on an ongoing debate on whether meta-learning can discover adaptable features and suggest that learning by sparse gradient descent is a powerful inductive bias for meta-learning systems.
Sequoia: A Software Framework to Unify Continual Learning Research
Aug 03, 2021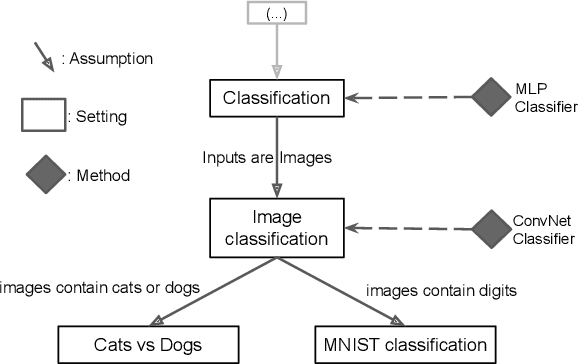
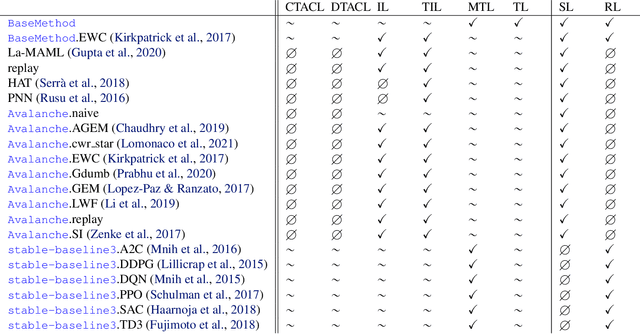
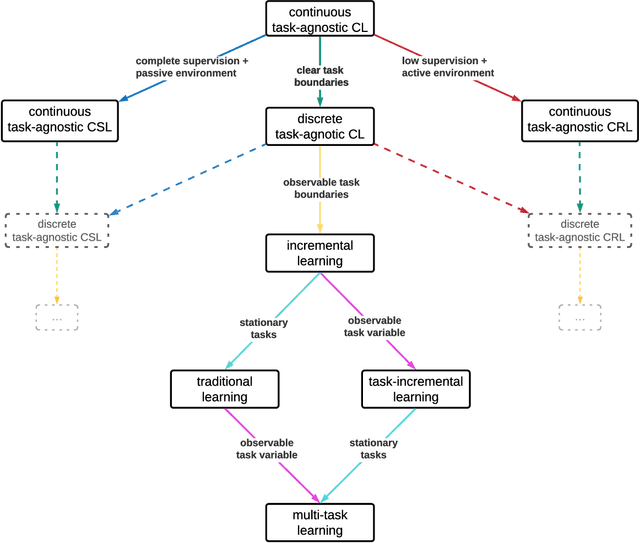
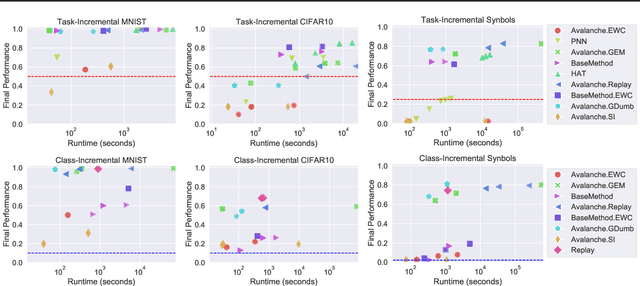
Abstract:The field of Continual Learning (CL) seeks to develop algorithms that accumulate knowledge and skills over time through interaction with non-stationary environments and data distributions. Measuring progress in CL can be difficult because a plethora of evaluation procedures (ettings) and algorithmic solutions (methods) have emerged, each with their own potentially disjoint set of assumptions about the CL problem. In this work, we view each setting as a set of assumptions. We then create a tree-shaped hierarchy of the research settings in CL, in which more general settings become the parents of those with more restrictive assumptions. This makes it possible to use inheritance to share and reuse research, as developing a method for a given setting also makes it directly applicable onto any of its children. We instantiate this idea as a publicly available software framework called Sequoia, which features a variety of settings from both the Continual Supervised Learning (CSL) and Continual Reinforcement Learning (CRL) domains. Sequoia also includes a growing suite of methods which are easy to extend and customize, in addition to more specialized methods from third-party libraries. We hope that this new paradigm and its first implementation can serve as a foundation for the unification and acceleration of research in CL. You can help us grow the tree by visiting www.github.com/lebrice/Sequoia.
A contrastive rule for meta-learning
Apr 19, 2021


Abstract:Meta-learning algorithms leverage regularities that are present on a set of tasks to speed up and improve the performance of a subsidiary learning process. Recent work on deep neural networks has shown that prior gradient-based learning of meta-parameters can greatly improve the efficiency of subsequent learning. Here, we present a biologically plausible meta-learning algorithm based on equilibrium propagation. Instead of explicitly differentiating the learning process, our contrastive meta-learning rule estimates meta-parameter gradients by executing the subsidiary process more than once. This avoids reversing the learning dynamics in time and computing second-order derivatives. In spite of this, and unlike previous first-order methods, our rule recovers an arbitrarily accurate meta-parameter update given enough compute. We establish theoretical bounds on its performance and present experiments on a set of standard benchmarks and neural network architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge