Aviary: training language agents on challenging scientific tasks

Solving complex real-world tasks requires cycles of actions and observations. This is particularly true in science, where tasks require many cycles of analysis, tool use, and experimentation. Language agents are promising for automating intellectual tasks in science because they can interact with tools via natural language or code. Yet their flexibility creates conceptual and practical challenges for software implementations, since agents may comprise non-standard components such as internal reasoning, planning, tool usage, as well as the inherent stochasticity of temperature-sampled language models. Here, we introduce Aviary, an extensible gymnasium for language agents. We formalize agents as policies solving language-grounded partially observable Markov decision processes, which we term language decision processes. We then implement five environments, including three challenging scientific environments: (1) manipulating DNA constructs for molecular cloning, (2) answering research questions by accessing scientific literature, and (3) engineering protein stability. These environments were selected for their focus on multi-step reasoning and their relevance to contemporary biology research. Finally, with online training and scaling inference-time compute, we show that language agents backed by open-source, non-frontier LLMs can match and exceed both frontier LLM agents and human experts on multiple tasks at up to 100x lower inference cost.

LAB-Bench: Measuring Capabilities of Language Models for Biology Research

There is widespread optimism that frontier Large Language Models (LLMs) and LLM-augmented systems have the potential to rapidly accelerate scientific discovery across disciplines. Today, many benchmarks exist to measure LLM knowledge and reasoning on textbook-style science questions, but few if any benchmarks are designed to evaluate language model performance on practical tasks required for scientific research, such as literature search, protocol planning, and data analysis. As a step toward building such benchmarks, we introduce the Language Agent Biology Benchmark (LAB-Bench), a broad dataset of over 2,400 multiple choice questions for evaluating AI systems on a range of practical biology research capabilities, including recall and reasoning over literature, interpretation of figures, access and navigation of databases, and comprehension and manipulation of DNA and protein sequences. Importantly, in contrast to previous scientific benchmarks, we expect that an AI system that can achieve consistently high scores on the more difficult LAB-Bench tasks would serve as a useful assistant for researchers in areas such as literature search and molecular cloning. As an initial assessment of the emergent scientific task capabilities of frontier language models, we measure performance of several against our benchmark and report results compared to human expert biology researchers. We will continue to update and expand LAB-Bench over time, and expect it to serve as a useful tool in the development of automated research systems going forward. A public subset of LAB-Bench is available for use at the following URL: https://huggingface.co/datasets/futurehouse/lab-bench

PaperQA: Retrieval-Augmented Generative Agent for Scientific Research

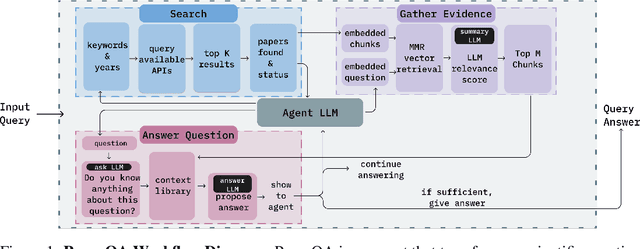
Large Language Models (LLMs) generalize well across language tasks, but suffer from hallucinations and uninterpretability, making it difficult to assess their accuracy without ground-truth. Retrieval-Augmented Generation (RAG) models have been proposed to reduce hallucinations and provide provenance for how an answer was generated. Applying such models to the scientific literature may enable large-scale, systematic processing of scientific knowledge. We present PaperQA, a RAG agent for answering questions over the scientific literature. PaperQA is an agent that performs information retrieval across full-text scientific articles, assesses the relevance of sources and passages, and uses RAG to provide answers. Viewing this agent as a question answering model, we find it exceeds performance of existing LLMs and LLM agents on current science QA benchmarks. To push the field closer to how humans perform research on scientific literature, we also introduce LitQA, a more complex benchmark that requires retrieval and synthesis of information from full-text scientific papers across the literature. Finally, we demonstrate PaperQA's matches expert human researchers on LitQA.

14 Examples of How LLMs Can Transform Materials Science and Chemistry: A Reflection on a Large Language Model Hackathon

Chemistry and materials science are complex. Recently, there have been great successes in addressing this complexity using data-driven or computational techniques. Yet, the necessity of input structured in very specific forms and the fact that there is an ever-growing number of tools creates usability and accessibility challenges. Coupled with the reality that much data in these disciplines is unstructured, the effectiveness of these tools is limited. Motivated by recent works that indicated that large language models (LLMs) might help address some of these issues, we organized a hackathon event on the applications of LLMs in chemistry, materials science, and beyond. This article chronicles the projects built as part of this hackathon. Participants employed LLMs for various applications, including predicting properties of molecules and materials, designing novel interfaces for tools, extracting knowledge from unstructured data, and developing new educational applications. The diverse topics and the fact that working prototypes could be generated in less than two days highlight that LLMs will profoundly impact the future of our fields. The rich collection of ideas and projects also indicates that the applications of LLMs are not limited to materials science and chemistry but offer potential benefits to a wide range of scientific disciplines.

Probability Theory without Bayes' Rule

Within the Kolmogorov theory of probability, Bayes' rule allows one to perform statistical inference by relating conditional probabilities to unconditional probabilities. As we show here, however, there is a continuous set of alternative inference rules that yield the same results, and that may have computational or practical advantages for certain problems. We formulate generalized axioms for probability theory, according to which the reverse conditional probability distribution P(B|A) is not specified by the forward conditional probability distribution P(A|B) and the marginals P(A) and P(B). Thus, in order to perform statistical inference, one must specify an additional "inference axiom," which relates P(B|A) to P(A|B), P(A), and P(B). We show that when Bayes' rule is chosen as the inference axiom, the axioms are equivalent to the classical Kolmogorov axioms. We then derive consistency conditions on the inference axiom, and thereby characterize the set of all possible rules for inference. The set of "first-order" inference axioms, defined as the set of axioms in which P(B|A) depends on the first power of P(A|B), is found to be a 1-simplex, with Bayes' rule at one of the extreme points. The other extreme point, the "inversion rule," is studied in depth.