Finite Sample Frequency Domain Identification

We study non-parametric frequency-domain system identification from a finite-sample perspective. We assume an open loop scenario where the excitation input is periodic and consider the Empirical Transfer Function Estimate (ETFE), where the goal is to estimate the frequency response at certain desired (evenly-spaced) frequencies, given input-output samples. We show that under sub-Gaussian colored noise (in time-domain) and stability assumptions, the ETFE estimates are concentrated around the true values. The error rate is of the order of $\mathcal{O}((d_{\mathrm{u}}+\sqrt{d_{\mathrm{u}}d_{\mathrm{y}}})\sqrt{M/N_{\mathrm{tot}}})$, where $N_{\mathrm{tot}}$ is the total number of samples, $M$ is the number of desired frequencies, and $d_{\mathrm{u}},\,d_{\mathrm{y}}$ are the dimensions of the input and output signals respectively. This rate remains valid for general irrational transfer functions and does not require a finite order state-space representation. By tuning $M$, we obtain a $N_{\mathrm{tot}}^{-1/3}$ finite-sample rate for learning the frequency response over all frequencies in the $ \mathcal{H}_{\infty}$ norm. Our result draws upon an extension of the Hanson-Wright inequality to semi-infinite matrices. We study the finite-sample behavior of ETFE in simulations.

Online Identification of Stochastic Continuous-Time Wiener Models Using Sampled Data

It is well known that ignoring the presence of stochastic disturbances in the identification of stochastic Wiener models leads to asymptotically biased estimators. On the other hand, optimal statistical identification, via likelihood-based methods, is sensitive to the assumptions on the data distribution and is usually based on relatively complex sequential Monte Carlo algorithms. We develop a simple recursive online estimation algorithm based on an output-error predictor, for the identification of continuous-time stochastic parametric Wiener models through stochastic approximation. The method is applicable to generic model parameterizations and, as demonstrated in the numerical simulation examples, it is robust with respect to the assumptions on the spectrum of the disturbance process.

Error Bounds for Kernel-Based Linear System Identification with Unknown Hyperparameters

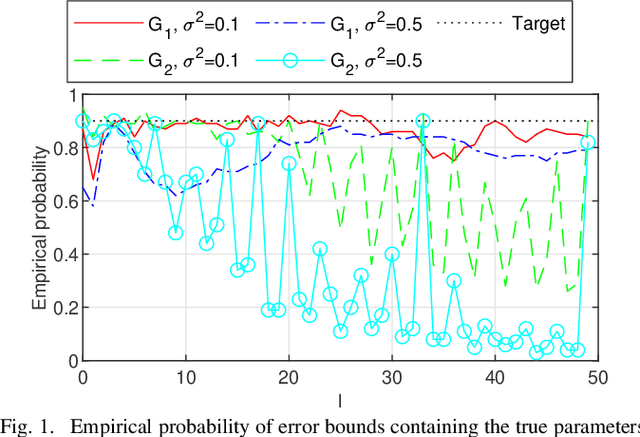
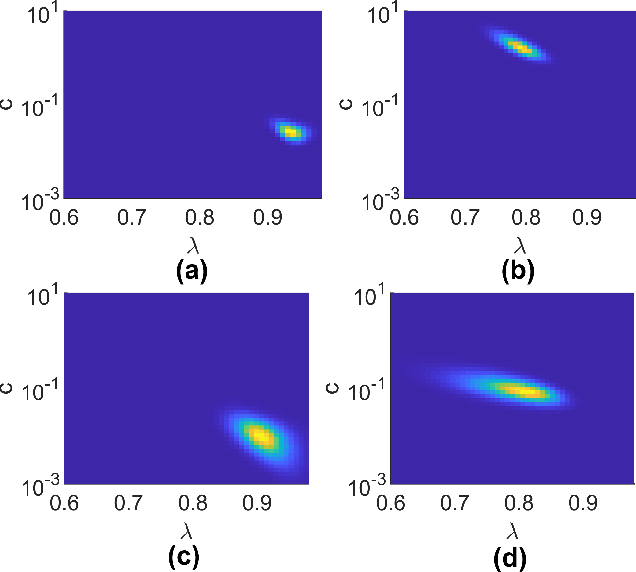
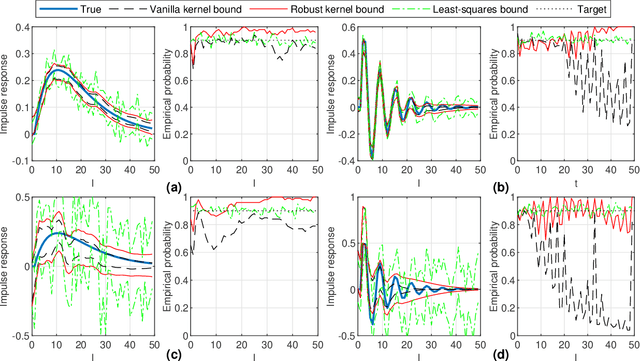
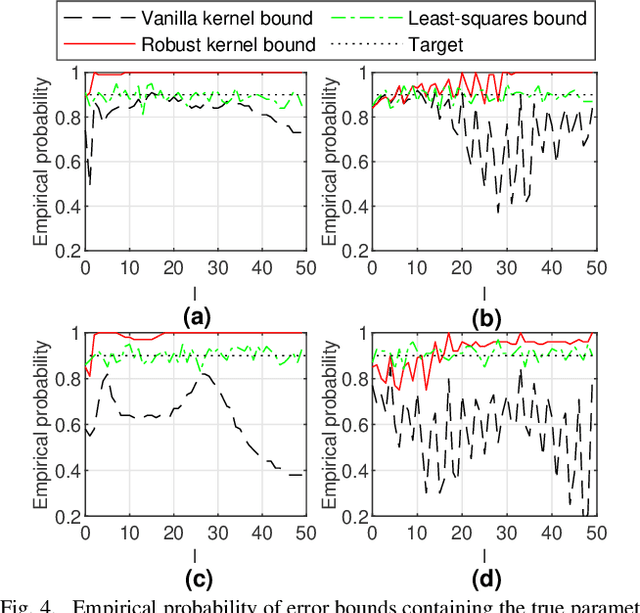
The kernel-based method has been successfully applied in linear system identification using stable kernel designs. From a Gaussian process perspective, it automatically provides probabilistic error bounds for the identified models from the posterior covariance, which are useful in robust and stochastic control. However, the error bounds require knowledge of the true hyperparameters in the kernel design and are demonstrated to be inaccurate with estimated hyperparameters for lightly damped systems or in the presence of high noise. In this work, we provide reliable quantification of the estimation error when the hyperparameters are unknown. The bounds are obtained by first constructing a high-probability set for the true hyperparameters from the marginal likelihood function and then finding the worst-case posterior covariance within the set. The proposed bound is proven to contain the true model with a high probability and its validity is verified in numerical simulation.

The Existence and Uniqueness of Solutions for Kernel-Based System Identification

The notion of reproducing kernel Hilbert space (RKHS) has emerged in system identification during the past decade. In the resulting framework, the impulse response estimation problem is formulated as a regularized optimization defined on an infinite-dimensional RKHS consisting of stable impulse responses. The consequent estimation problem is well-defined under the central assumption that the convolution operators restricted to the RKHS are continuous linear functionals. Moreover, according to this assumption, the representer theorem hold, and therefore, the impulse response can be estimated by solving a finite-dimensional program. Thus, the continuity feature plays a significant role in kernel-based system identification. This paper shows that this central assumption is guaranteed to be satisfied in considerably general situations, namely when the kernel is an integrable function and the input signal is bounded. Furthermore, the strong convexity of the optimization problem and the continuity property of the convolution operators imply that the kernel-based system identification admits a unique solution. Consequently, it follows that kernel-based system identification is a well-defined approach.

Regret Analysis of Online Gradient Descent-based Iterative Learning Control with Model Mismatch

In Iterative Learning Control (ILC), a sequence of feedforward control actions is generated at each iteration on the basis of partial model knowledge and past measurements with the goal of steering the system toward a desired reference trajectory. This is framed here as an online learning task, where the decision-maker takes sequential decisions by solving a sequence of optimization problems having only partial knowledge of the cost functions. Having established this connection, the performance of an online gradient-descent based scheme using inexact gradient information is analyzed in the setting of dynamic and static regret, standard measures in online learning. Fundamental limitations of the scheme and its integration with adaptation mechanisms are further investigated, followed by numerical simulations on a benchmark ILC problem.

Infinite-Dimensional Sparse Learning in Linear System Identification

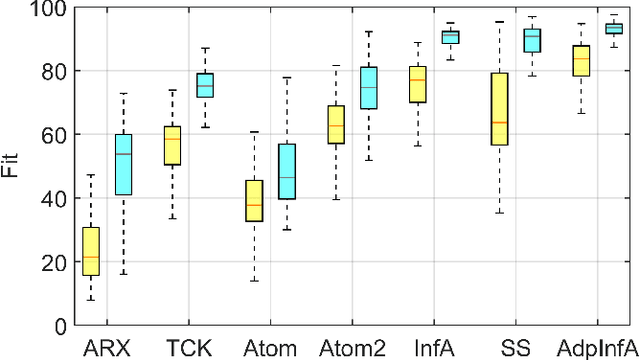
Regularized methods have been widely applied to system identification problems without known model structures. This paper proposes an infinite-dimensional sparse learning algorithm based on atomic norm regularization. Atomic norm regularization decomposes the transfer function into first-order atomic models and solves a group lasso problem that selects a sparse set of poles and identifies the corresponding coefficients. The difficulty in solving the problem lies in the fact that there are an infinite number of possible atomic models. This work proposes a greedy algorithm that generates new candidate atomic models maximizing the violation of the optimality condition of the existing problem. This algorithm is able to solve the infinite-dimensional group lasso problem with high precision. The algorithm is further extended to reduce the bias and reject false positives in pole location estimation by iteratively reweighted adaptive group lasso and complementary pairs stability selection respectively. Numerical results demonstrate that the proposed algorithm performs better than benchmark parameterized and regularized methods in terms of both impulse response fitting and pole location estimation.

Kernel-Based Identification with Frequency Domain Side-Information

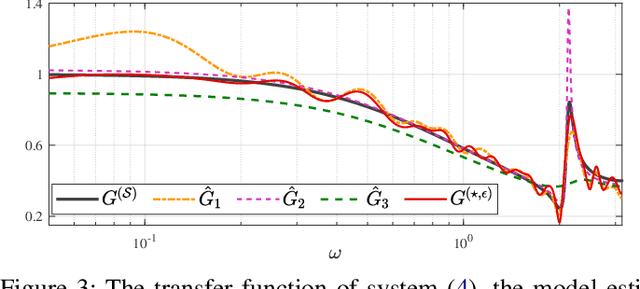
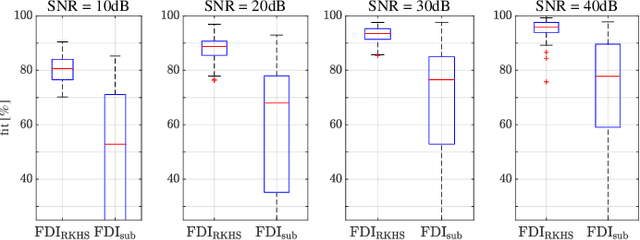
This paper discusses the problem of system identification when frequency domain side-information is available. Initially, we consider the case where the side-information is provided as the $\mathcal{H}_{\infty}$-norm of the system being bounded by a given scalar. This framework allows considering different forms of frequency domain side-information, such as the dissipativity of the system. We propose a nonparametric identification approach for estimating the impulse response of the system under the given side-information. The estimation problem is formulated as a constrained optimization in a stable reproducing kernel Hilbert space, where suitable constraints are considered for incorporating the desired frequency domain features. The resulting optimization has an infinite-dimensional feasible set with an infinite number of constraints. We show that this problem is a well-defined convex program with a unique solution. We propose a heuristic that tightly approximates this unique solution. The proposed approach is equivalent to solving a finite-dimensional convex quadratically constrained quadratic program. The efficiency of the discussed method is verified by several numerical examples.

Physics-informed linear regression is a competitive approach compared to Machine Learning methods in building MPC

Because physics-based building models are difficult to obtain as each building is individual, there is an increasing interest in generating models suitable for building MPC directly from measurement data. Machine learning methods have been widely applied to this problem and validated mostly in simulation; there are, however, few studies on a direct comparison of different models or validation in real buildings to be found in the literature. Methods that are indeed validated in application often lead to computationally complex non-convex optimization problems. Here we compare physics-informed Autoregressive-Moving-Average with Exogenous Inputs (ARMAX) models to Machine Learning models based on Random Forests and Input Convex Neural Networks and the resulting convex MPC schemes in experiments on a practical building application with the goal of minimizing energy consumption while maintaining occupant comfort, and in a numerical case study. We demonstrate that Predictive Control in general leads to savings between 26% and 49% of heating and cooling energy, compared to the building's baseline hysteresis controller. Moreover, we show that all model types lead to satisfactory control performance in terms of constraint satisfaction and energy reduction. However, we also see that the physics-informed ARMAX models have a lower computational burden, and a superior sample efficiency compared to the Machine Learning based models. Moreover, even if abundant training data is available, the ARMAX models have a significantly lower prediction error than the Machine Learning models, which indicates that the encoded physics-based prior of the former cannot independently be found by the latter.

Distributed Model Predictive Control of Buildings and Energy Hubs

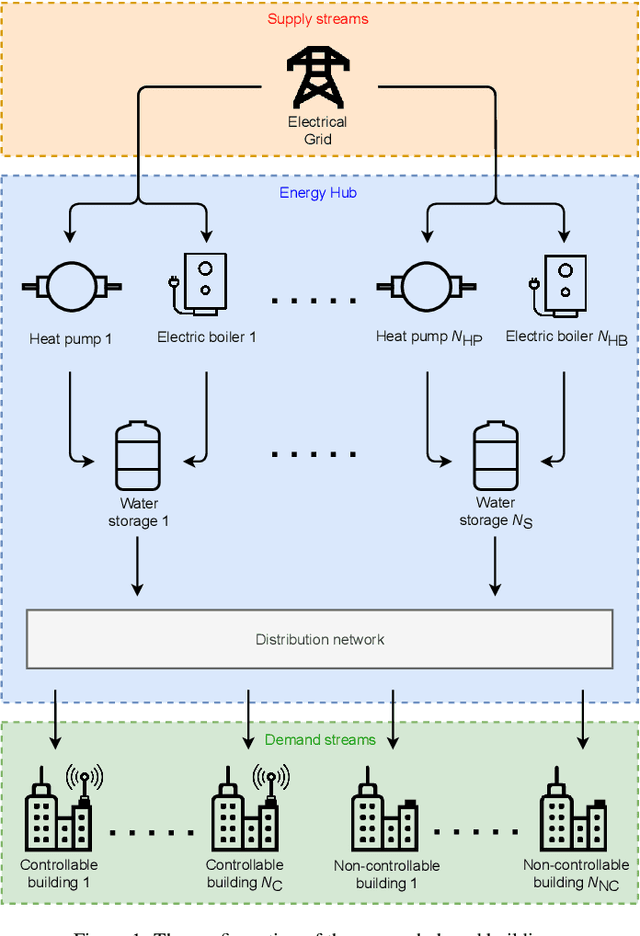
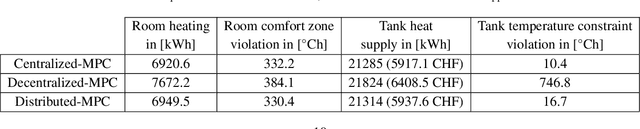
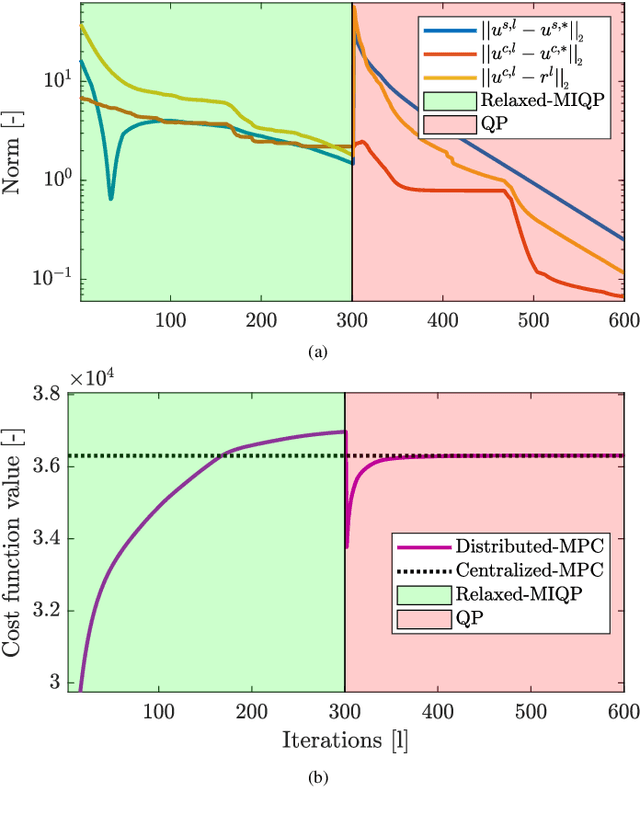
Model predictive control (MPC) strategies can be applied to the coordination of energy hubs to reduce their energy consumption. Despite the effectiveness of these techniques, their potential for energy savings are potentially underutilized due to the fact that energy demands are often assumed to be fixed quantities rather than controlled dynamic variables. The joint optimization of energy hubs and buildings' energy management systems can result in higher energy savings. This paper investigates how different MPC strategies perform on energy management systems in buildings and energy hubs. We first discuss two MPC approaches; centralized and decentralized. While the centralized control strategy offers optimal performance, its implementation is computationally prohibitive and raises privacy concerns. On the other hand, the decentralized control approach, which offers ease of implementation, displays significantly lower performance. We propose a third strategy, distributed control based on dual decomposition, which has the advantages of both approaches. Numerical case studies and comparisons demonstrate that the performance of distributed control is close to the performance of the centralized case, while maintaining a significantly lower computational burden, especially in large-scale scenarios with many agents. Finally, we validate and verify the reliability of the proposed method through an experiment on a full-scale energy hub system in the NEST demonstrator in D\"{u}bendorf, Switzerland.

On Robustness of Kernel-Based Regularized System Identification

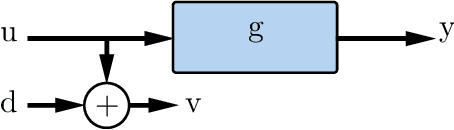
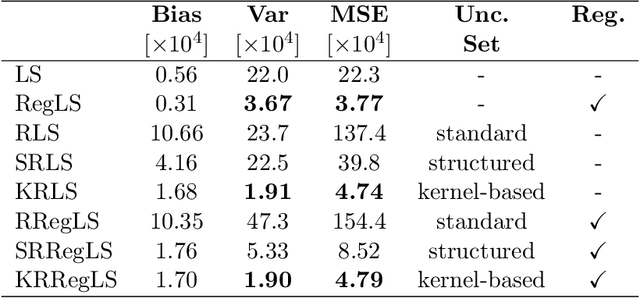
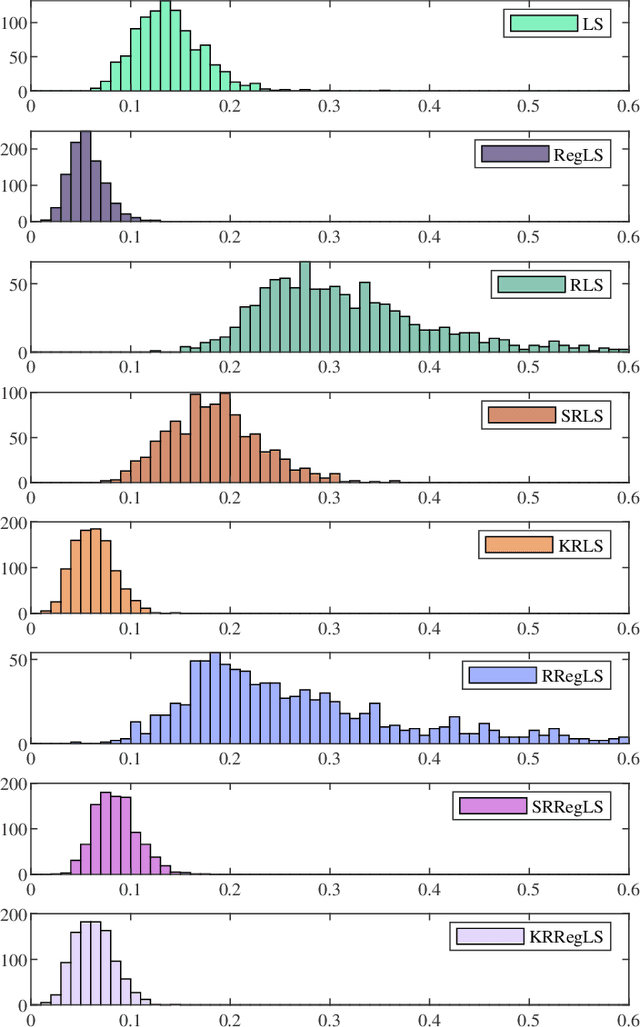
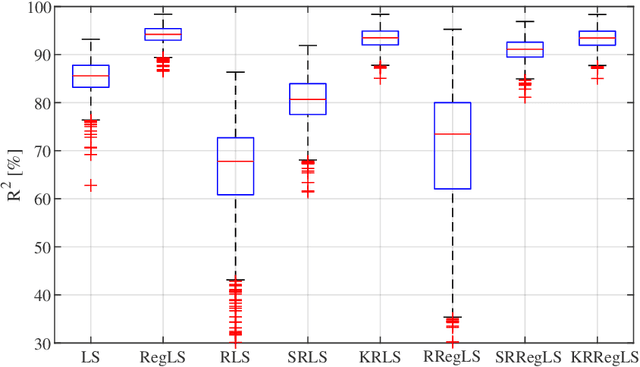
This paper presents a novel feature of the kernel-based system identification method. We prove that the regularized kernel-based approach for the estimation of a finite impulse response is equivalent to a robust least-squares problem with a particular uncertainty set defined in terms of the kernel matrix, and thus, it is called kernel-based uncertainty set. We provide a theoretical foundation for the robustness of the kernel-based approach to input disturbances. Based on robust and regularized least-squares methods, different formulations of system identification are considered, where the kernel-based uncertainty set is employed in some of them. We apply these methods to a case where the input measurements are subject to disturbances. Subsequently, we perform extensive numerical experiments and compare the results to examine the impact of utilizing kernel-based uncertainty sets in the identification procedure. The numerical experiments confirm that the robust least square identification approach with the kernel-based uncertainty set improves the robustness of the estimation to the input disturbances.