On Robustness of Kernel-Based Regularized System Identification
Paper and Code
May 26, 2021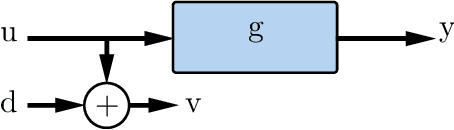
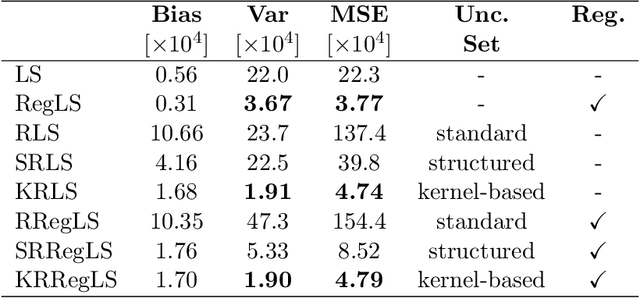
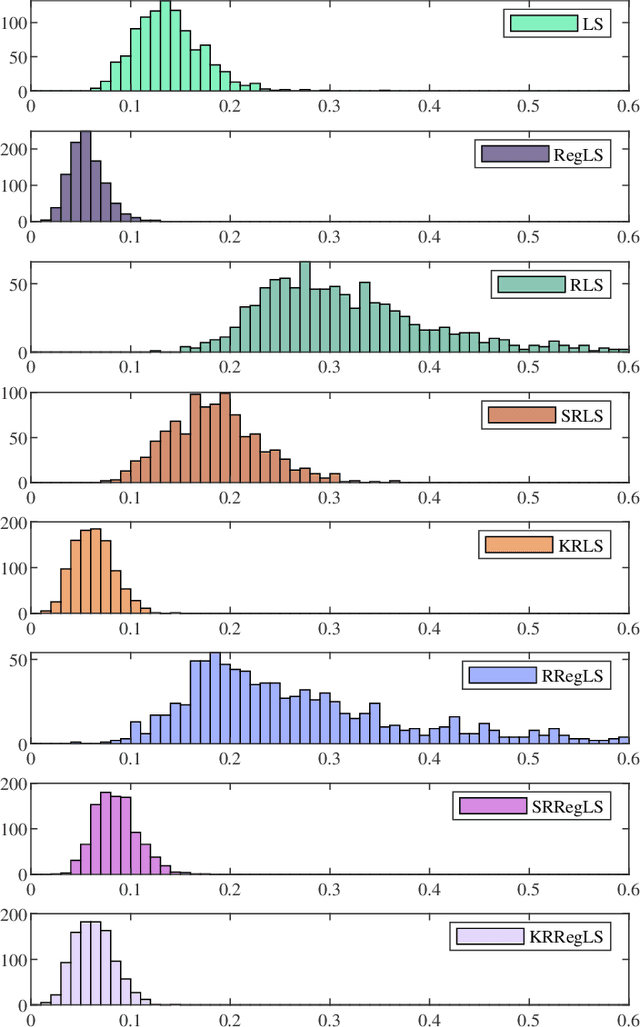
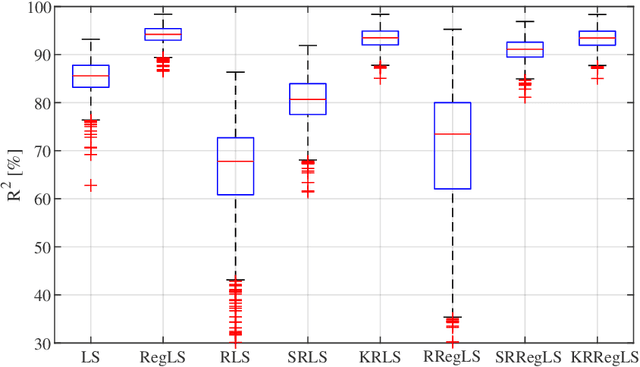
This paper presents a novel feature of the kernel-based system identification method. We prove that the regularized kernel-based approach for the estimation of a finite impulse response is equivalent to a robust least-squares problem with a particular uncertainty set defined in terms of the kernel matrix, and thus, it is called kernel-based uncertainty set. We provide a theoretical foundation for the robustness of the kernel-based approach to input disturbances. Based on robust and regularized least-squares methods, different formulations of system identification are considered, where the kernel-based uncertainty set is employed in some of them. We apply these methods to a case where the input measurements are subject to disturbances. Subsequently, we perform extensive numerical experiments and compare the results to examine the impact of utilizing kernel-based uncertainty sets in the identification procedure. The numerical experiments confirm that the robust least square identification approach with the kernel-based uncertainty set improves the robustness of the estimation to the input disturbances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge