Kernel-Based Identification with Frequency Domain Side-Information

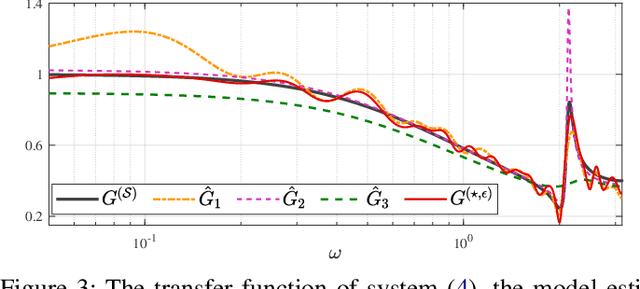
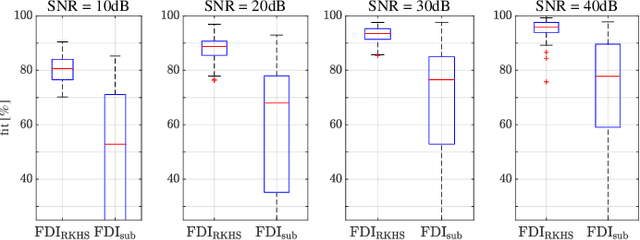
This paper discusses the problem of system identification when frequency domain side-information is available. Initially, we consider the case where the side-information is provided as the $\mathcal{H}_{\infty}$-norm of the system being bounded by a given scalar. This framework allows considering different forms of frequency domain side-information, such as the dissipativity of the system. We propose a nonparametric identification approach for estimating the impulse response of the system under the given side-information. The estimation problem is formulated as a constrained optimization in a stable reproducing kernel Hilbert space, where suitable constraints are considered for incorporating the desired frequency domain features. The resulting optimization has an infinite-dimensional feasible set with an infinite number of constraints. We show that this problem is a well-defined convex program with a unique solution. We propose a heuristic that tightly approximates this unique solution. The proposed approach is equivalent to solving a finite-dimensional convex quadratically constrained quadratic program. The efficiency of the discussed method is verified by several numerical examples.