Infinite-Dimensional Sparse Learning in Linear System Identification
Paper and Code
Mar 28, 2022
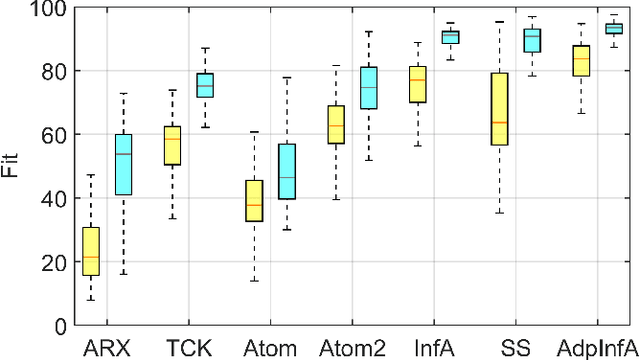


Regularized methods have been widely applied to system identification problems without known model structures. This paper proposes an infinite-dimensional sparse learning algorithm based on atomic norm regularization. Atomic norm regularization decomposes the transfer function into first-order atomic models and solves a group lasso problem that selects a sparse set of poles and identifies the corresponding coefficients. The difficulty in solving the problem lies in the fact that there are an infinite number of possible atomic models. This work proposes a greedy algorithm that generates new candidate atomic models maximizing the violation of the optimality condition of the existing problem. This algorithm is able to solve the infinite-dimensional group lasso problem with high precision. The algorithm is further extended to reduce the bias and reject false positives in pole location estimation by iteratively reweighted adaptive group lasso and complementary pairs stability selection respectively. Numerical results demonstrate that the proposed algorithm performs better than benchmark parameterized and regularized methods in terms of both impulse response fitting and pole location estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge