Low-Rank Matrix Regression via Least-Angle Regression

Low-rank matrix regression is a fundamental problem in data science with various applications in systems and control. Nuclear norm regularization has been widely applied to solve this problem due to its convexity. However, it suffers from high computational complexity and the inability to directly specify the rank. This work introduces a novel framework for low-rank matrix regression that addresses both unstructured and Hankel matrices. By decomposing the low-rank matrix into rank-1 bases, the problem is reformulated as an infinite-dimensional sparse learning problem. The least-angle regression (LAR) algorithm is then employed to solve this problem efficiently. For unstructured matrices, a closed-form LAR solution is derived with equivalence to a normalized nuclear norm regularization problem. For Hankel matrices, a real-valued polynomial basis reformulation enables effective LAR implementation. Two numerical examples in network modeling and system realization demonstrate that the proposed approach significantly outperforms the nuclear norm method in terms of estimation accuracy and computational efficiency.

Gaussian Process-Based Prediction and Control of Hammerstein-Wiener Systems

This work investigates data-driven prediction and control of Hammerstein-Wiener systems using physics-informed Gaussian process models. Data-driven prediction algorithms have been developed for structured nonlinear systems based on Willems' fundamental lemma. However, existing frameworks cannot treat output nonlinearities and require a dictionary of basis functions for Hammerstein systems. In this work, an implicit predictor structure is considered, leveraging the multi-step-ahead ARX structure for the linear part of the model. This implicit function is learned by Gaussian process regression with kernel functions designed from Gaussian process priors for the nonlinearities. The linear model parameters are estimated as hyperparameters by assuming a stable spline hyperprior. The implicit Gaussian process model provides explicit output prediction by optimizing selected optimality criteria. The model is also applied to receding horizon control with the expected control cost and chance constraint satisfaction guarantee. Numerical results demonstrate that the proposed prediction and control algorithms are superior to black-box Gaussian process models.

Error Bounds for Kernel-Based Linear System Identification with Unknown Hyperparameters

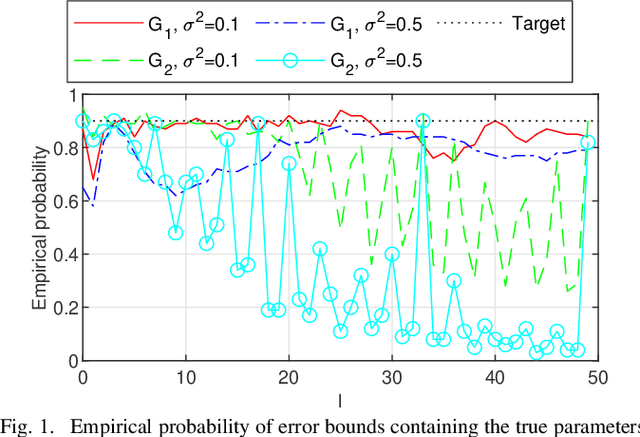
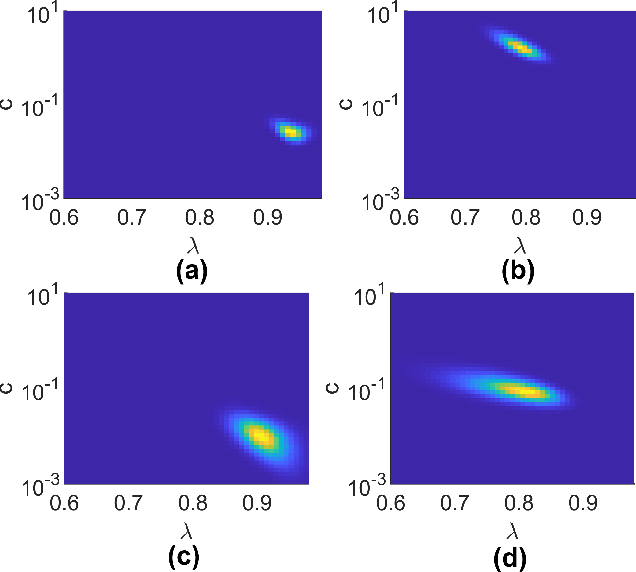
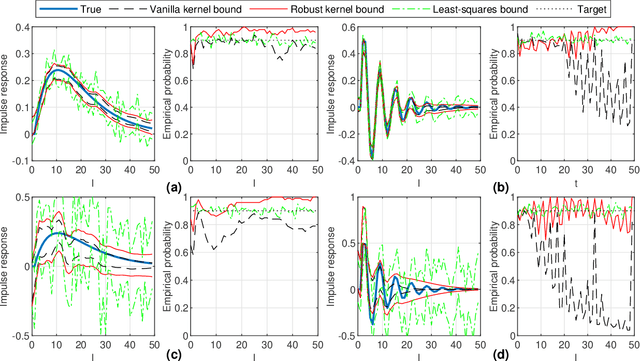
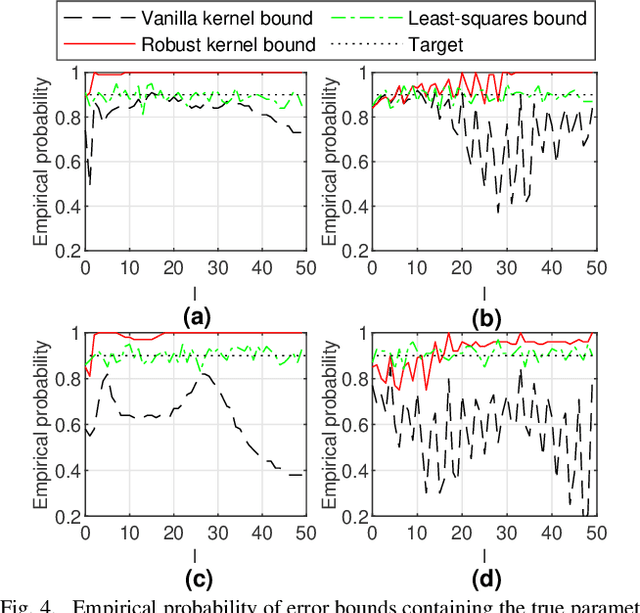
The kernel-based method has been successfully applied in linear system identification using stable kernel designs. From a Gaussian process perspective, it automatically provides probabilistic error bounds for the identified models from the posterior covariance, which are useful in robust and stochastic control. However, the error bounds require knowledge of the true hyperparameters in the kernel design and are demonstrated to be inaccurate with estimated hyperparameters for lightly damped systems or in the presence of high noise. In this work, we provide reliable quantification of the estimation error when the hyperparameters are unknown. The bounds are obtained by first constructing a high-probability set for the true hyperparameters from the marginal likelihood function and then finding the worst-case posterior covariance within the set. The proposed bound is proven to contain the true model with a high probability and its validity is verified in numerical simulation.

Infinite-Dimensional Sparse Learning in Linear System Identification

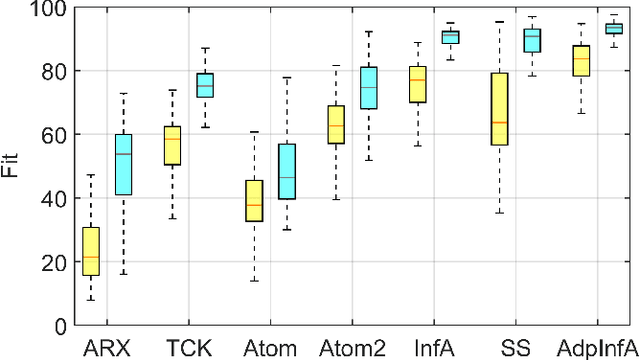
Regularized methods have been widely applied to system identification problems without known model structures. This paper proposes an infinite-dimensional sparse learning algorithm based on atomic norm regularization. Atomic norm regularization decomposes the transfer function into first-order atomic models and solves a group lasso problem that selects a sparse set of poles and identifies the corresponding coefficients. The difficulty in solving the problem lies in the fact that there are an infinite number of possible atomic models. This work proposes a greedy algorithm that generates new candidate atomic models maximizing the violation of the optimality condition of the existing problem. This algorithm is able to solve the infinite-dimensional group lasso problem with high precision. The algorithm is further extended to reduce the bias and reject false positives in pole location estimation by iteratively reweighted adaptive group lasso and complementary pairs stability selection respectively. Numerical results demonstrate that the proposed algorithm performs better than benchmark parameterized and regularized methods in terms of both impulse response fitting and pole location estimation.