ADMM-based Adaptive Sampling Strategy for Nonholonomic Mobile Robotic Sensor Networks
Paper and Code
Jan 27, 2021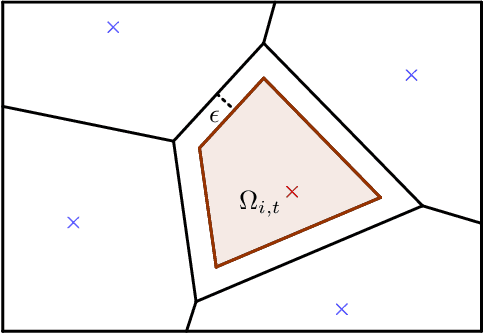
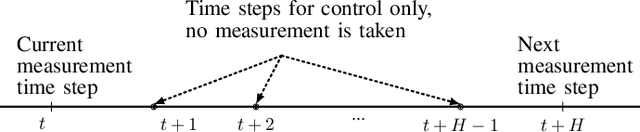
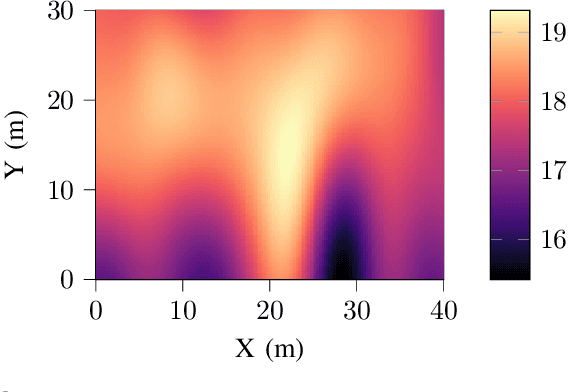

This paper discusses the adaptive sampling problem in a nonholonomic mobile robotic sensor network for efficiently monitoring a spatial field. It is proposed to employ Gaussian process to model a spatial phenomenon and predict it at unmeasured positions, which enables the sampling optimization problem to be formulated by the use of the log determinant of a predicted covariance matrix at next sampling locations. The control, movement and nonholonomic dynamics constraints of the mobile sensors are also considered in the adaptive sampling optimization problem. In order to tackle the nonlinearity and nonconvexity of the objective function in the optimization problem we first exploit the linearized alternating direction method of multipliers (L-ADMM) method that can effectively simplify the objective function, though it is computationally expensive since a nonconvex problem needs to be solved exactly in each iteration. We then propose a novel approach called the successive convexified ADMM (SC-ADMM) that sequentially convexify the nonlinear dynamic constraints so that the original optimization problem can be split into convex subproblems. It is noted that both the L-ADMM algorithm and our SC-ADMM approach can solve the sampling optimization problem in either a centralized or a distributed manner. We validated the proposed approaches in 1000 experiments in a synthetic environment with a real-world dataset, where the obtained results suggest that both the L-ADMM and SC- ADMM techniques can provide good accuracy for the monitoring purpose. However, our proposed SC-ADMM approach computationally outperforms the L-ADMM counterpart, demonstrating its better practicality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge