Rotating spiders and reflecting dogs: a class conditional approach to learning data augmentation distributions
Paper and Code
Jun 07, 2021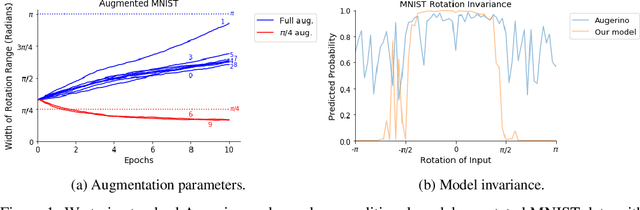
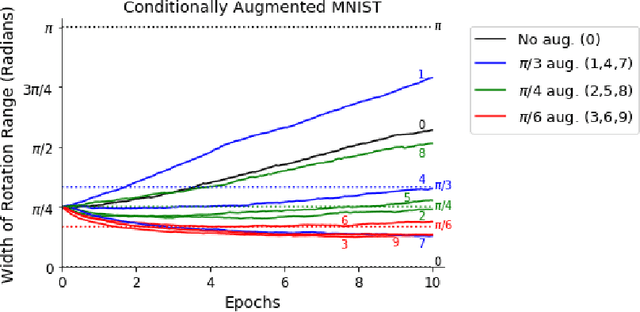
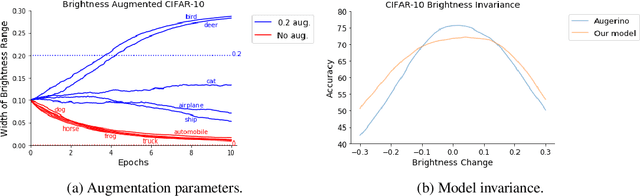
Building invariance to non-meaningful transformations is essential to building efficient and generalizable machine learning models. In practice, the most common way to learn invariance is through data augmentation. There has been recent interest in the development of methods that learn distributions on augmentation transformations from the training data itself. While such approaches are beneficial since they are responsive to the data, they ignore the fact that in many situations the range of transformations to which a model needs to be invariant changes depending on the particular class input belongs to. For example, if a model needs to be able to predict whether an image contains a starfish or a dog, we may want to apply random rotations to starfish images during training (since these do not have a preferred orientation), but we would not want to do this to images of dogs. In this work we introduce a method by which we can learn class conditional distributions on augmentation transformations. We give a number of examples where our methods learn different non-meaningful transformations depending on class and further show how our method can be used as a tool to probe the symmetries intrinsic to a potentially complex dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge