Hodgelets: Localized Spectral Representations of Flows on Simplicial Complexes

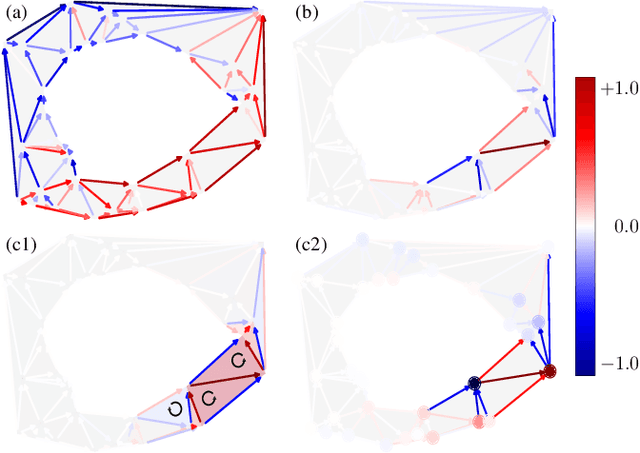
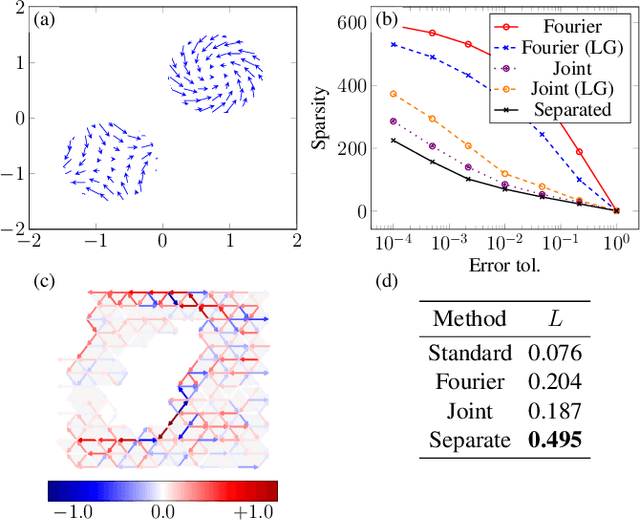
We develop wavelet representations for edge-flows on simplicial complexes, using ideas rooted in combinatorial Hodge theory and spectral graph wavelets. We first show that the Hodge Laplacian can be used in lieu of the graph Laplacian to construct a family of wavelets for higher-order signals on simplicial complexes. Then, we refine this idea to construct wavelets that respect the Hodge-Helmholtz decomposition. For these Hodgelets, familiar notions of curl-free and divergence-free flows from vector calculus are preserved. We characterize the representational quality of our Hodgelets for edge flows in terms of frame bounds and demonstrate the use of these spectral wavelets for sparse representation of edge flows on real and synthetic data.