Outlier Detection for Trajectories via Flow-embeddings

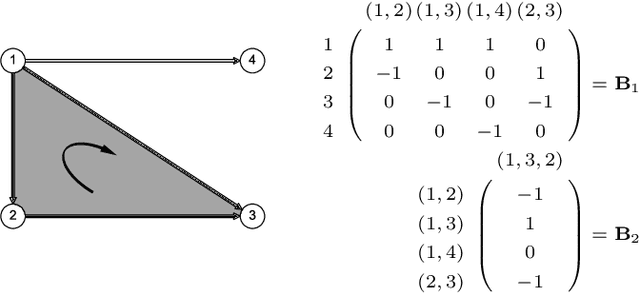
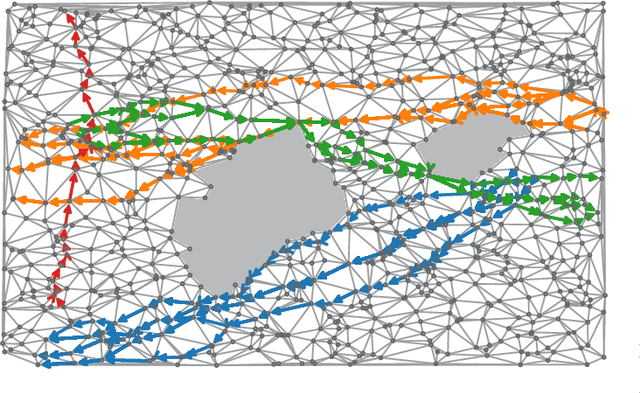
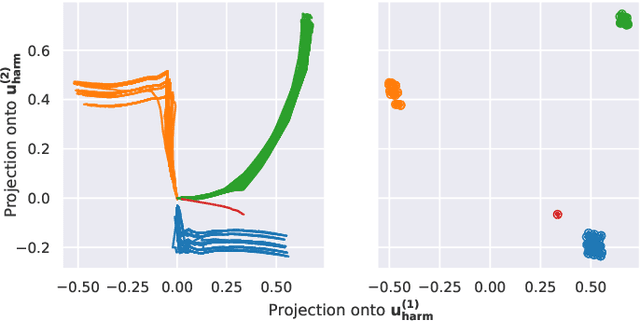
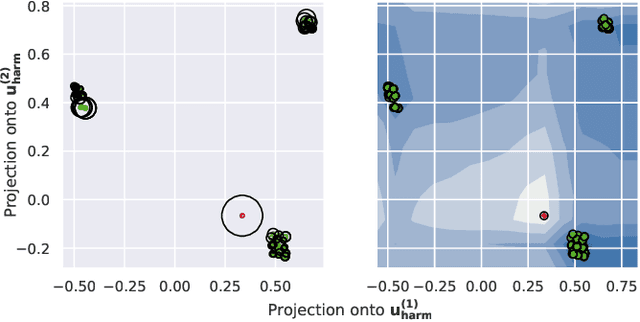
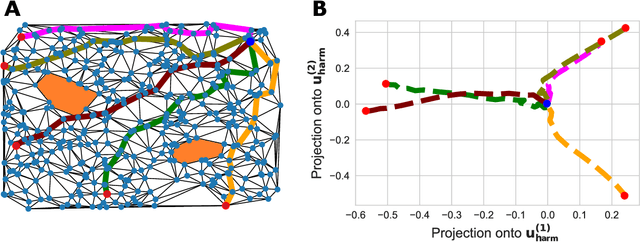
We propose a method to detect outliers in empirically observed trajectories on a discrete or discretized manifold modeled by a simplicial complex. Our approach is similar to spectral embeddings such as diffusion-maps and Laplacian eigenmaps, that construct vertex embeddings from the eigenvectors of the graph Laplacian associated with low eigenvalues. Here we consider trajectories as edge-flow vectors defined on a simplicial complex, a higher-order generalization of graphs, and use the Hodge 1-Laplacian of the simplicial complex to derive embeddings of these edge-flows. By projecting trajectory vectors onto the eigenspace of the Hodge 1-Laplacian associated to small eigenvalues, we can characterize the behavior of the trajectories relative to the homology of the complex, which corresponds to holes in the underlying space. This enables us to classify trajectories based on simply interpretable, low-dimensional statistics. We show how this technique can single out trajectories that behave (topologically) different compared to typical trajectories, and illustrate the performance of our approach with both synthetic and empirical data.

Signal processing on simplicial complexes

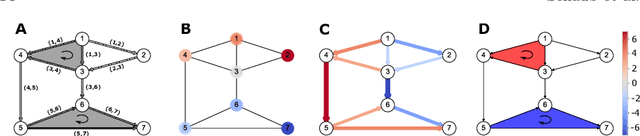
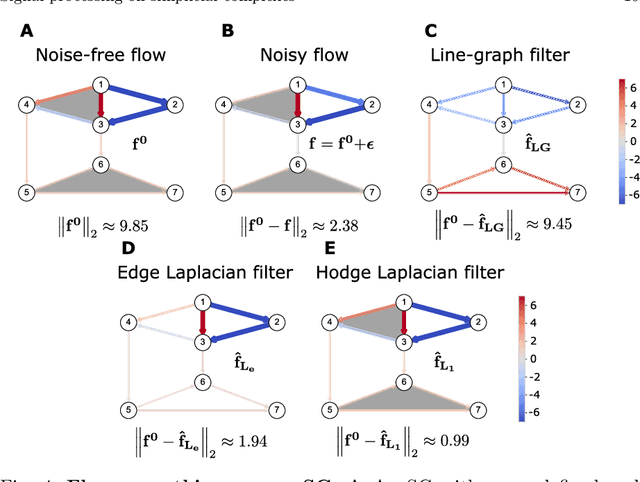
Higher-order networks have so far been considered primarily in the context of studying the structure of complex systems, i.e., the higher-order or multi-way relations connecting the constituent entities. More recently, a number of studies have considered dynamical processes that explicitly account for such higher-order dependencies, e.g., in the context of epidemic spreading processes or opinion formation. In this chapter, we focus on a closely related, but distinct third perspective: how can we use higher-order relationships to process signals and data supported on higher-order network structures. In particular, we survey how ideas from signal processing of data supported on regular domains, such as time series or images, can be extended to graphs and simplicial complexes. We discuss Fourier analysis, signal denoising, signal interpolation, and nonlinear processing through neural networks based on simplicial complexes. Key to our developments is the Hodge Laplacian matrix, a multi-relational operator that leverages the special structure of simplicial complexes and generalizes desirable properties of the Laplacian matrix in graph signal processing.

Signal Processing on Higher-Order Networks: Livin' on the Edge ... and Beyond

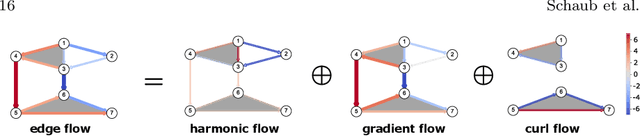
This tutorial paper presents a didactic treatment of the emerging topic of signal processing on higher-order networks. Drawing analogies from discrete and graph signal processing, we introduce the building blocks for processing data on simplicial complexes and hypergraphs, two common abstractions of higher-order networks that can incorporate polyadic relationships.We provide basic introductions to simplicial complexes and hypergraphs, making special emphasis on the concepts needed for processing signals on them. Leveraging these concepts, we discuss Fourier analysis, signal denoising, signal interpolation, node embeddings, and non-linear processing through neural networks in these two representations of polyadic relational structures. In the context of simplicial complexes, we specifically focus on signal processing using the Hodge Laplacian matrix, a multi-relational operator that leverages the special structure of simplicial complexes and generalizes desirable properties of the Laplacian matrix in graph signal processing. For hypergraphs, we present both matrix and tensor representations, and discuss the trade-offs in adopting one or the other. We also highlight limitations and potential research avenues, both to inform practitioners and to motivate the contribution of new researchers to the area.