Outlier Detection for Trajectories via Flow-embeddings
Paper and Code
Nov 25, 2021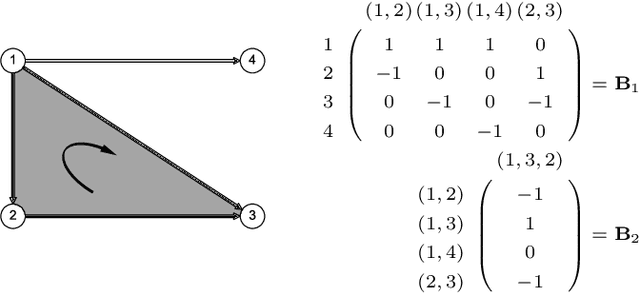
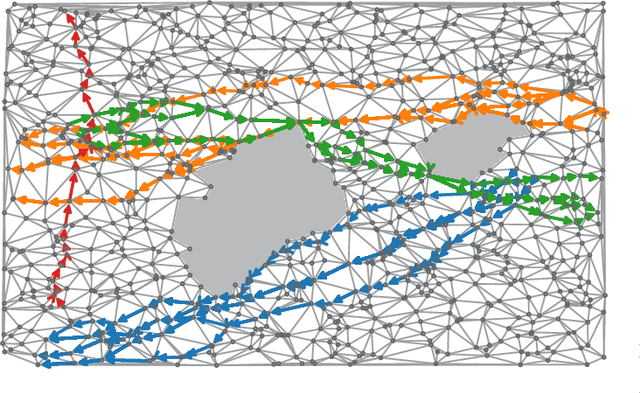
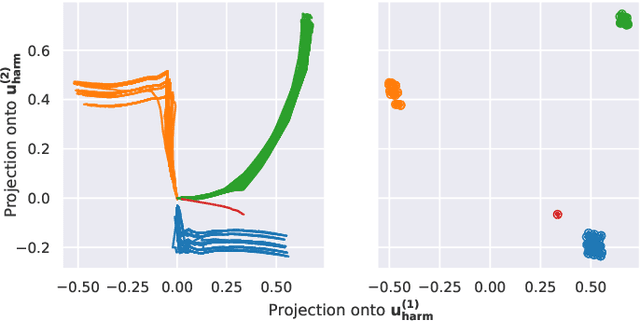
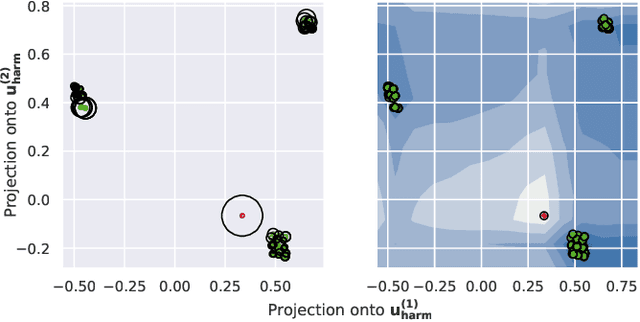
We propose a method to detect outliers in empirically observed trajectories on a discrete or discretized manifold modeled by a simplicial complex. Our approach is similar to spectral embeddings such as diffusion-maps and Laplacian eigenmaps, that construct vertex embeddings from the eigenvectors of the graph Laplacian associated with low eigenvalues. Here we consider trajectories as edge-flow vectors defined on a simplicial complex, a higher-order generalization of graphs, and use the Hodge 1-Laplacian of the simplicial complex to derive embeddings of these edge-flows. By projecting trajectory vectors onto the eigenspace of the Hodge 1-Laplacian associated to small eigenvalues, we can characterize the behavior of the trajectories relative to the homology of the complex, which corresponds to holes in the underlying space. This enables us to classify trajectories based on simply interpretable, low-dimensional statistics. We show how this technique can single out trajectories that behave (topologically) different compared to typical trajectories, and illustrate the performance of our approach with both synthetic and empirical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge