Explaining the Impact of Training on Vision Models via Activation Clustering

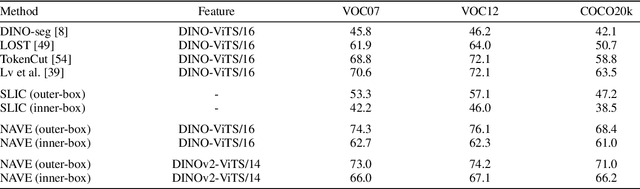
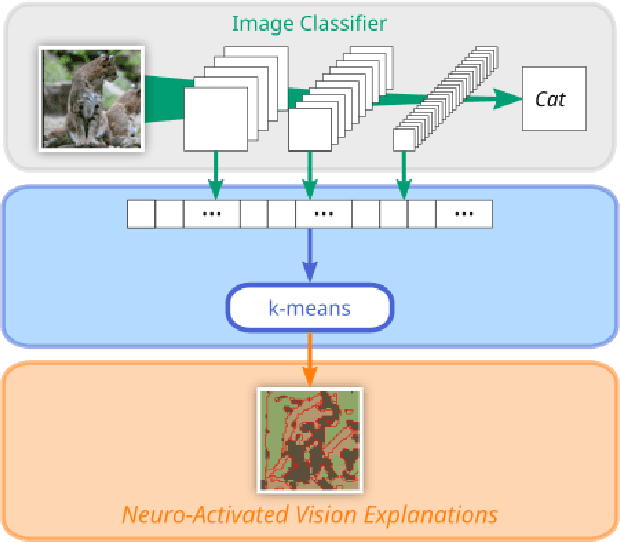
Recent developments in the field of explainable artificial intelligence (XAI) for vision models investigate the information extracted by their feature encoder. We contribute to this effort and propose Neuro-Activated Vision Explanations (NAVE), which extracts the information captured by the encoder by clustering the feature activations of the frozen network to be explained. The method does not aim to explain the model's prediction but to answer questions such as which parts of the image are processed similarly or which information is kept in deeper layers. Experimentally, we leverage NAVE to show that the training dataset and the level of supervision affect which concepts are captured. In addition, our method reveals the impact of registers on vision transformers (ViT) and the information saturation caused by the watermark Clever Hans effect in the training set.

Leveraging Activations for Superpixel Explanations

Saliency methods have become standard in the explanation toolkit of deep neural networks. Recent developments specific to image classifiers have investigated region-based explanations with either new methods or by adapting well-established ones using ad-hoc superpixel algorithms. In this paper, we aim to avoid relying on these segmenters by extracting a segmentation from the activations of a deep neural network image classifier without fine-tuning the network. Our so-called Neuro-Activated Superpixels (NAS) can isolate the regions of interest in the input relevant to the model's prediction, which boosts high-threshold weakly supervised object localization performance. This property enables the semi-supervised semantic evaluation of saliency methods. The aggregation of NAS with existing saliency methods eases their interpretation and reveals the inconsistencies of the widely used area under the relevance curve metric.

Efficient Radiation Treatment Planning based on Voxel Importance

Optimization is a time-consuming part of radiation treatment planning. We propose to reduce the optimization problem by only using a representative subset of informative voxels. This way, we improve planning efficiency while maintaining or enhancing the plan quality. To reduce the computational complexity of the optimization problem, we propose to subsample the set of voxels via importance sampling. We derive a sampling distribution based on an importance score that we obtain from pre-solving an easy optimization problem involving a simplified probing objective. By solving a reduced version of the original optimization problem using this subset, we effectively reduce the problem's size and computational demands while accounting for regions in which satisfactory dose deliveries are challenging. In contrast to other stochastic (sub-)sampling methods, our technique only requires a single sampling step to define a reduced optimization problem. This problem can be efficiently solved using established solvers. Empirical experiments on open benchmark data highlight substantially reduced optimization times, up to 50 times faster than the original ones, for intensity-modulated radiation therapy (IMRT), all while upholding plan quality comparable to traditional methods. Our approach has the potential to significantly accelerate radiation treatment planning by addressing its inherent computational challenges. We reduce the treatment planning time by reducing the size of the optimization problem rather than improving the optimization method. Our efforts are thus complementary to much of the previous developments.

Ising on the Graph: Task-specific Graph Subsampling via the Ising Model

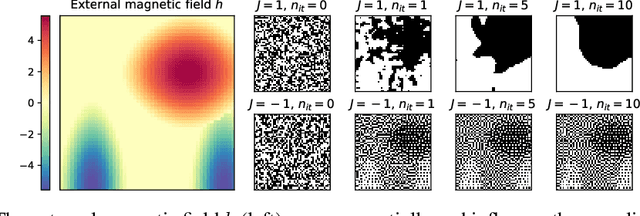
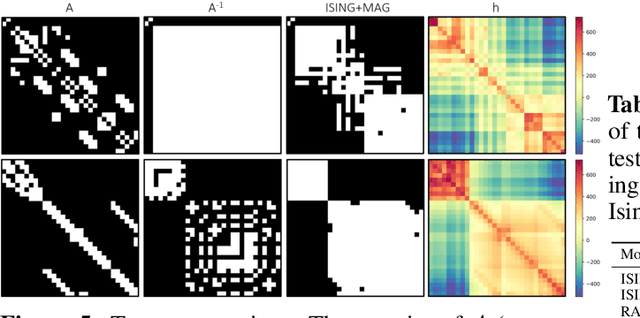
Reducing a graph while preserving its overall structure is an important problem with many applications. Typically, the reduction approaches either remove edges (sparsification) or merge nodes (coarsening) in an unsupervised way with no specific downstream task in mind. In this paper, we present an approach for subsampling graph structures using an Ising model defined on either the nodes or edges and learning the external magnetic field of the Ising model using a graph neural network. Our approach is task-specific as it can learn how to reduce a graph for a specific downstream task in an end-to-end fashion. The utilized loss function of the task does not even have to be differentiable. We showcase the versatility of our approach on three distinct applications: image segmentation, 3D shape sparsification, and sparse approximate matrix inverse determination.

On Feynman--Kac training of partial Bayesian neural networks

Recently, partial Bayesian neural networks (pBNNs), which only consider a subset of the parameters to be stochastic, were shown to perform competitively with full Bayesian neural networks. However, pBNNs are often multi-modal in the latent-variable space and thus challenging to approximate with parametric models. To address this problem, we propose an efficient sampling-based training strategy, wherein the training of a pBNN is formulated as simulating a Feynman--Kac model. We then describe variations of sequential Monte Carlo samplers that allow us to simultaneously estimate the parameters and the latent posterior distribution of this model at a tractable computational cost. We show on various synthetic and real-world datasets that our proposed training scheme outperforms the state of the art in terms of predictive performance.

Privacy Amplification via Importance Sampling

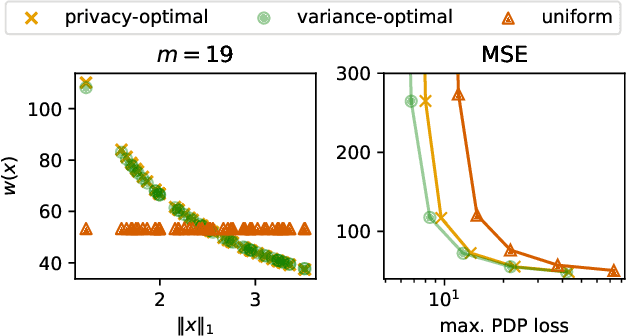
We examine the privacy-enhancing properties of subsampling a data set via importance sampling as a pre-processing step for differentially private mechanisms. This extends the established privacy amplification by subsampling result to importance sampling where each data point is weighted by the reciprocal of its selection probability. The implications for privacy of weighting each point are not obvious. On the one hand, a lower selection probability leads to a stronger privacy amplification. On the other hand, the higher the weight, the stronger the influence of the point on the output of the mechanism in the event that the point does get selected. We provide a general result that quantifies the trade-off between these two effects. We show that heterogeneous sampling probabilities can lead to both stronger privacy and better utility than uniform subsampling while retaining the subsample size. In particular, we formulate and solve the problem of privacy-optimal sampling, that is, finding the importance weights that minimize the expected subset size subject to a given privacy budget. Empirically, we evaluate the privacy, efficiency, and accuracy of importance sampling-based privacy amplification on the example of k-means clustering.

Self-Supervised Siamese Autoencoders

Fully supervised models often require large amounts of labeled training data, which tends to be costly and hard to acquire. In contrast, self-supervised representation learning reduces the amount of labeled data needed for achieving the same or even higher downstream performance. The goal is to pre-train deep neural networks on a self-supervised task such that afterwards the networks are able to extract meaningful features from raw input data. These features are then used as inputs in downstream tasks, such as image classification. Previously, autoencoders and Siamese networks such as SimSiam have been successfully employed in those tasks. Yet, challenges remain, such as matching characteristics of the features (e.g., level of detail) to the given task and data set. In this paper, we present a new self-supervised method that combines the benefits of Siamese architectures and denoising autoencoders. We show that our model, called SidAE (Siamese denoising autoencoder), outperforms two self-supervised baselines across multiple data sets, settings, and scenarios. Crucially, this includes conditions in which only a small amount of labeled data is available.

Archetypal Analysis++: Rethinking the Initialization Strategy

Archetypal analysis is a matrix factorization method with convexity constraints. Due to local minima, a good initialization is essential. Frequently used initialization methods yield either sub-optimal starting points or are prone to get stuck in poor local minima. In this paper, we propose archetypal analysis++ (AA++), a probabilistic initialization strategy for archetypal analysis that sequentially samples points based on their influence on the objective, similar to $k$-means++. In fact, we argue that $k$-means++ already approximates the proposed initialization method. Furthermore, we suggest to adapt an efficient Monte Carlo approximation of $k$-means++ to AA++. In an extensive empirical evaluation of 13 real-world data sets of varying sizes and dimensionalities and considering two pre-processing strategies, we show that AA++ almost consistently outperforms all baselines, including the most frequently used ones.

Principled Interpolation in Normalizing Flows

Generative models based on normalizing flows are very successful in modeling complex data distributions using simpler ones. However, straightforward linear interpolations show unexpected side effects, as interpolation paths lie outside the area where samples are observed. This is caused by the standard choice of Gaussian base distributions and can be seen in the norms of the interpolated samples. This observation suggests that correcting the norm should generally result in better interpolations, but it is not clear how to correct the norm in an unambiguous way. In this paper, we solve this issue by enforcing a fixed norm and, hence, change the base distribution, to allow for a principled way of interpolation. Specifically, we use the Dirichlet and von Mises-Fisher base distributions. Our experimental results show superior performance in terms of bits per dimension, Fr\'echet Inception Distance (FID), and Kernel Inception Distance (KID) scores for interpolation, while maintaining the same generative performance.