Biarchetype analysis: simultaneous learning of observations and features based on extremes

A new exploratory technique called biarchetype analysis is defined. We extend archetype analysis to find the archetypes of both observations and features simultaneously. The idea of this new unsupervised machine learning tool is to represent observations and features by instances of pure types (biarchetypes) that can be easily interpreted as they are mixtures of observations and features. Furthermore, the observations and features are expressed as mixtures of the biarchetypes, which also helps understand the structure of the data. We propose an algorithm to solve biarchetype analysis. We show that biarchetype analysis offers advantages over biclustering, especially in terms of interpretability. This is because byarchetypes are extreme instances as opposed to the centroids returned by biclustering, which favors human understanding. Biarchetype analysis is applied to several machine learning problems to illustrate its usefulness.

Ordinal classification for interval-valued data and interval-valued functional data

The aim of ordinal classification is to predict the ordered labels of the output from a set of observed inputs. Interval-valued data refers to data in the form of intervals. For the first time, interval-valued data and interval-valued functional data are considered as inputs in an ordinal classification problem. Six ordinal classifiers for interval data and interval-valued functional data are proposed. Three of them are parametric, one of them is based on ordinal binary decompositions and the other two are based on ordered logistic regression. The other three methods are based on the use of distances between interval data and kernels on interval data. One of the methods uses the weighted $k$-nearest-neighbor technique for ordinal classification. Another method considers kernel principal component analysis plus an ordinal classifier. And the sixth method, which is the method that performs best, uses a kernel-induced ordinal random forest. They are compared with na\"ive approaches in an extensive experimental study with synthetic and original real data sets, about human global development, and weather data. The results show that considering ordering and interval-valued information improves the accuracy. The source code and data sets are available at https://github.com/aleixalcacer/OCFIVD.

Finding archetypal patterns for binary questionnaires

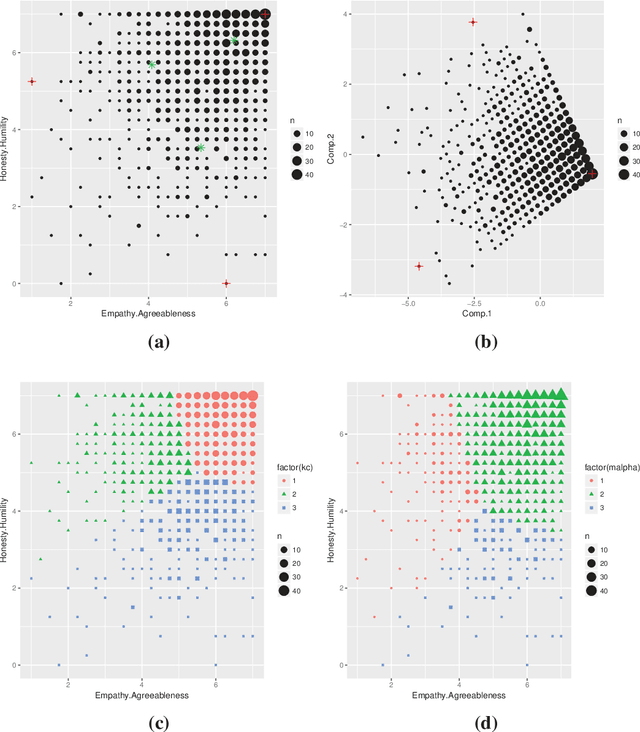
Archetypal analysis is an exploratory tool that explains a set of observations as mixtures of pure (extreme) patterns. If the patterns are actual observations of the sample, we refer to them as archetypoids. For the first time, we propose to use archetypoid analysis for binary observations. This tool can contribute to the understanding of a binary data set, as in the multivariate case. We illustrate the advantages of the proposed methodology in a simulation study and two applications, one exploring objects (rows) and the other exploring items (columns). One is related to determining student skill set profiles and the other to describing item response functions.

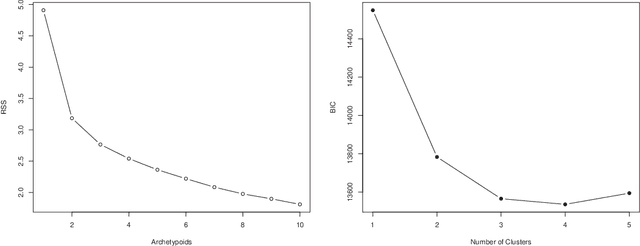
Robust multivariate and functional archetypal analysis with application to financial time series analysis

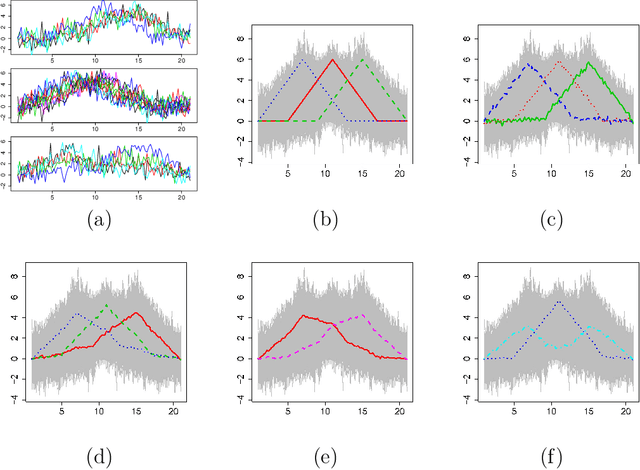
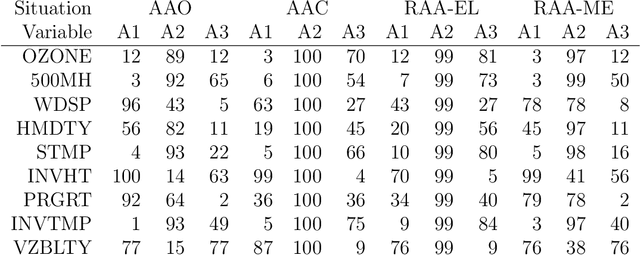
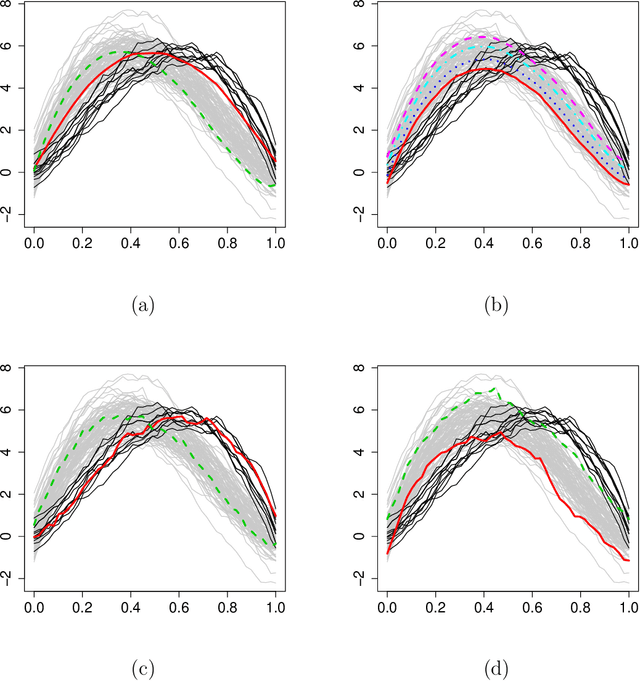
Archetypal analysis approximates data by means of mixtures of actual extreme cases (archetypoids) or archetypes, which are a convex combination of cases in the data set. Archetypes lie on the boundary of the convex hull. This makes the analysis very sensitive to outliers. A robust methodology by means of M-estimators for classical multivariate and functional data is proposed. This unsupervised methodology allows complex data to be understood even by non-experts. The performance of the new procedure is assessed in a simulation study, where a comparison with a previous methodology for the multivariate case is also carried out, and our proposal obtains favorable results. Finally, robust bivariate functional archetypoid analysis is applied to a set of companies in the S\&P 500 described by two time series of stock quotes. A new graphic representation is also proposed to visualize the results. The analysis shows how the information can be easily interpreted and how even non-experts can gain a qualitative understanding of the data.

Functional archetype and archetypoid analysis

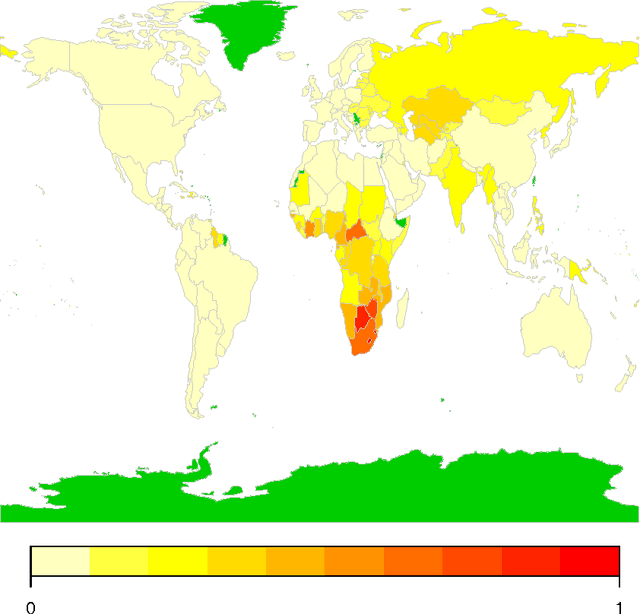
Archetype and archetypoid analysis can be extended to functional data. Each function is represented as a mixture of actual observations (functional archetypoids) or functional archetypes, which are a mixture of observations in the data set. Well-known Canadian temperature data are used to illustrate the analysis developed. Computational methods are proposed for performing these analyses, based on the coefficients of a basis. Unlike a previous attempt to compute functional archetypes, which was only valid for an orthogonal basis, the proposed methodology can be used for any basis. It is computationally less demanding than the simple approach of discretizing the functions. Multivariate functional archetype and archetypoid analysis are also introduced and applied in an interesting problem about the study of human development around the world over the last 50 years. These tools can contribute to the understanding of a functional data set, as in the multivariate case.