John Aston
SurvSurf: a partially monotonic neural network for first-hitting time prediction of intermittently observed discrete and continuous sequential events
Apr 07, 2025Abstract:We propose a neural-network based survival model (SurvSurf) specifically designed for direct and simultaneous probabilistic prediction of the first hitting time of sequential events from baseline. Unlike existing models, SurvSurf is theoretically guaranteed to never violate the monotonic relationship between the cumulative incidence functions of sequential events, while allowing nonlinear influence from predictors. It also incorporates implicit truths for unobserved intermediate events in model fitting, and supports both discrete and continuous time and events. We also identified a variant of the Integrated Brier Score (IBS) that showed robust correlation with the mean squared error (MSE) between the true and predicted probabilities by accounting for implied truths about the missing intermediate events. We demonstrated the superiority of SurvSurf compared to modern and traditional predictive survival models in two simulated datasets and two real-world datasets, using MSE, the more robust IBS and by measuring the extent of monotonicity violation.
Hidden Talents of the Variational Autoencoder
Apr 04, 2018



Abstract:Variational autoencoders (VAE) represent a popular, flexible form of deep generative model that can be stochastically fit to samples from a given random process using an information-theoretic variational bound on the true underlying distribution. Once so-obtained, the model can be putatively used to generate new samples from this distribution, or to provide a low-dimensional latent representation of existing samples. While quite effective in numerous application domains, certain important mechanisms which govern the behavior of the VAE are obfuscated by the intractable integrals and resulting stochastic approximations involved. Moreover, as a highly non-convex model, it remains unclear exactly how minima of the underlying energy relate to original design purposes. We attempt to better quantify these issues by analyzing a series of tractable special cases of increasing complexity. In doing so, we unveil interesting connections with more traditional dimensionality reduction models, as well as an intrinsic yet underappreciated propensity for robustly dismissing sparse outliers when estimating latent manifolds. With respect to the latter, we demonstrate that the VAE can be viewed as the natural evolution of recent robust PCA models, capable of learning nonlinear manifolds of unknown dimension obscured by gross corruptions.
Divide-and-Conquer with Sequential Monte Carlo
Jun 30, 2015


Abstract:We propose a novel class of Sequential Monte Carlo (SMC) algorithms, appropriate for inference in probabilistic graphical models. This class of algorithms adopts a divide-and-conquer approach based upon an auxiliary tree-structured decomposition of the model of interest, turning the overall inferential task into a collection of recursively solved sub-problems. The proposed method is applicable to a broad class of probabilistic graphical models, including models with loops. Unlike a standard SMC sampler, the proposed Divide-and-Conquer SMC employs multiple independent populations of weighted particles, which are resampled, merged, and propagated as the method progresses. We illustrate empirically that this approach can outperform standard methods in terms of the accuracy of the posterior expectation and marginal likelihood approximations. Divide-and-Conquer SMC also opens up novel parallel implementation options and the possibility of concentrating the computational effort on the most challenging sub-problems. We demonstrate its performance on a Markov random field and on a hierarchical logistic regression problem.
Monotonicity of Fitness Landscapes and Mutation Rate Control
Sep 04, 2012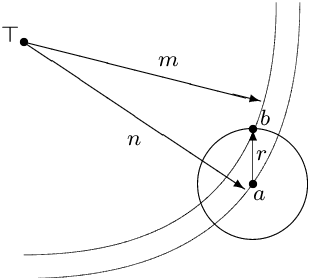
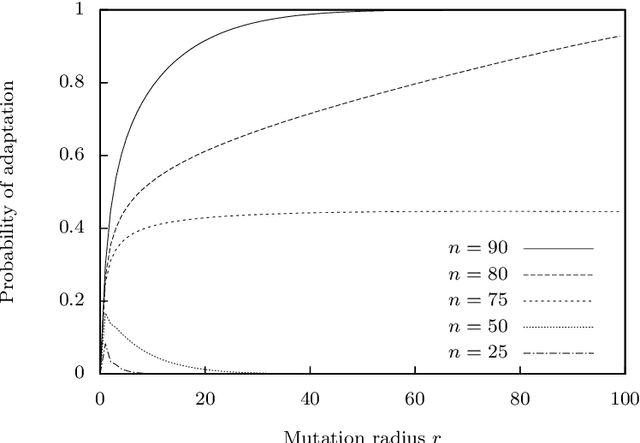
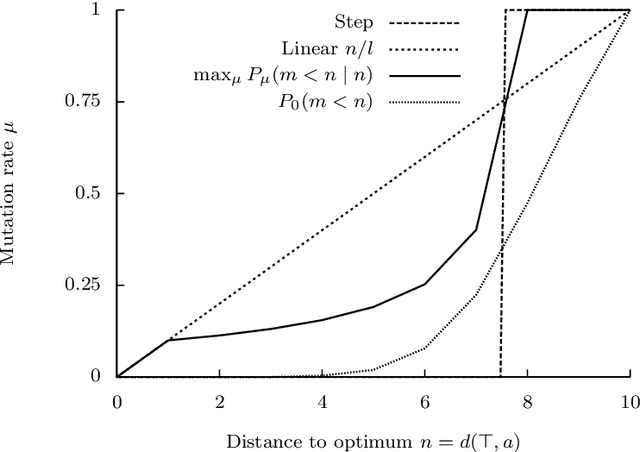
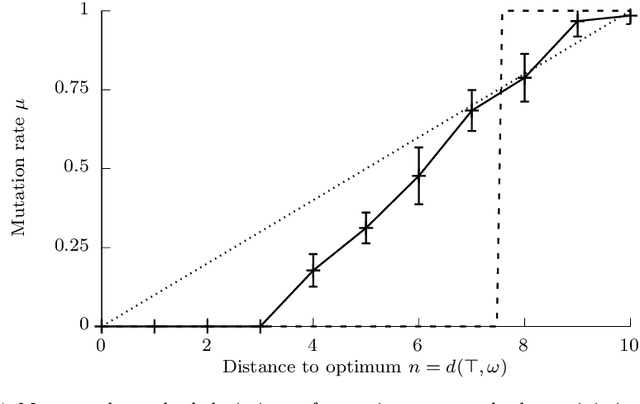
Abstract:The typical view in evolutionary biology is that mutation rates are minimised. Contrary to that view, studies in combinatorial optimisation and search have shown a clear advantage of using variable mutation rates as a control parameter to optimise the performance of evolutionary algorithms. Ronald Fisher's work is the basis of much biological theory in this area. He used Euclidean geometry of continuous, infinite phenotypic spaces to study the relation between mutation size and expected fitness of the offspring. Here we develop a general theory of optimal mutation rate control that is based on the alternative geometry of discrete and finite spaces of DNA sequences. We define the monotonic properties of fitness landscapes, which allows us to relate fitness to the topology of genotypes and mutation size. First, we consider the case of a perfectly monotonic fitness landscape, in which the optimal mutation rate control functions can be derived exactly or approximately depending on additional constraints of the problem. Then we consider the general case of non-monotonic landscapes. We use the ideas of local and weak monotonicity to show that optimal mutation rate control functions exist in any such landscape and that they resemble control functions in a monotonic landscape at least in some neighbourhood of a fitness maximum. Generally, optimal mutation rates increase when fitness decreases, and the increase of mutation rate is more rapid in landscapes that are less monotonic (more rugged). We demonstrate these relationships by obtaining and analysing approximately optimal mutation rate control functions in 115 complete landscapes of binding scores between DNA sequences and transcription factors. We discuss the relevance of these findings to living organisms, including the phenomenon of stress-induced mutagenesis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge