Optimal measures and Markov transition kernels

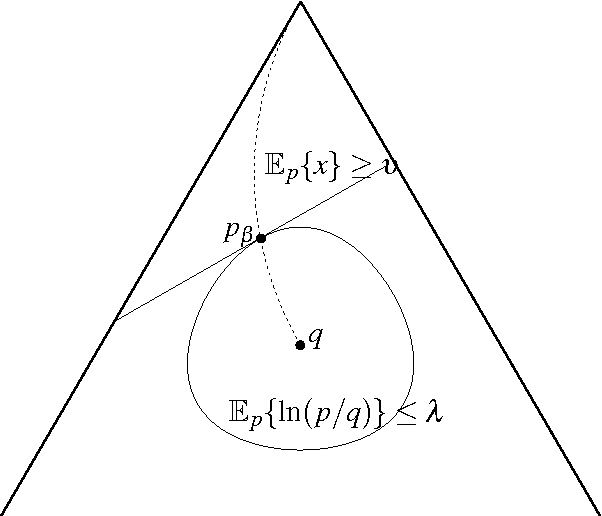
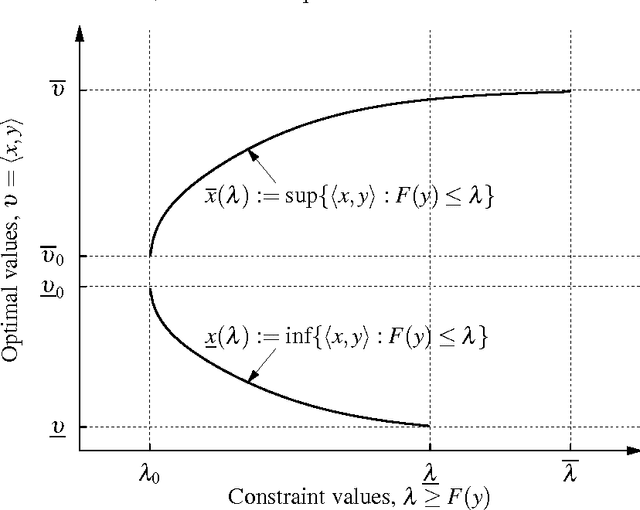
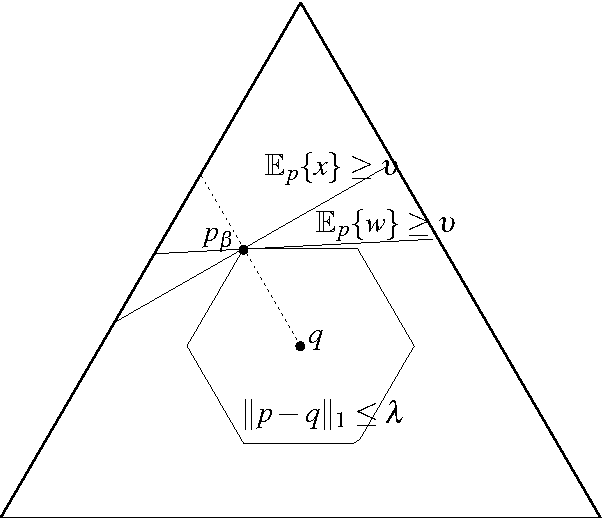
We study optimal solutions to an abstract optimization problem for measures, which is a generalization of classical variational problems in information theory and statistical physics. In the classical problems, information and relative entropy are defined using the Kullback-Leibler divergence, and for this reason optimal measures belong to a one-parameter exponential family. Measures within such a family have the property of mutual absolute continuity. Here we show that this property characterizes other families of optimal positive measures if a functional representing information has a strictly convex dual. Mutual absolute continuity of optimal probability measures allows us to strictly separate deterministic and non-deterministic Markov transition kernels, which play an important role in theories of decisions, estimation, control, communication and computation. We show that deterministic transitions are strictly sub-optimal, unless information resource with a strictly convex dual is unconstrained. For illustration, we construct an example where, unlike non-deterministic, any deterministic kernel either has negatively infinite expected utility (unbounded expected error) or communicates infinite information.

Monotonicity of Fitness Landscapes and Mutation Rate Control

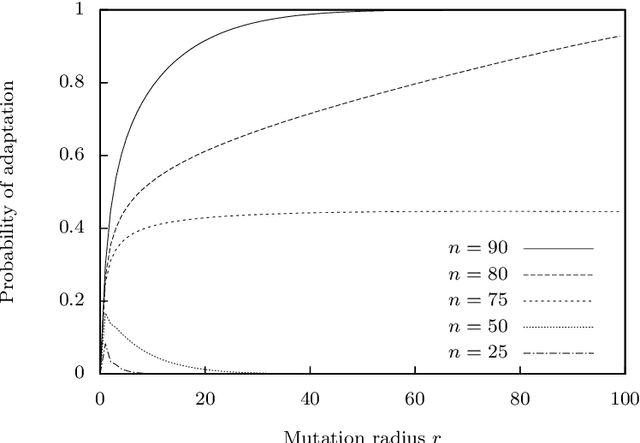
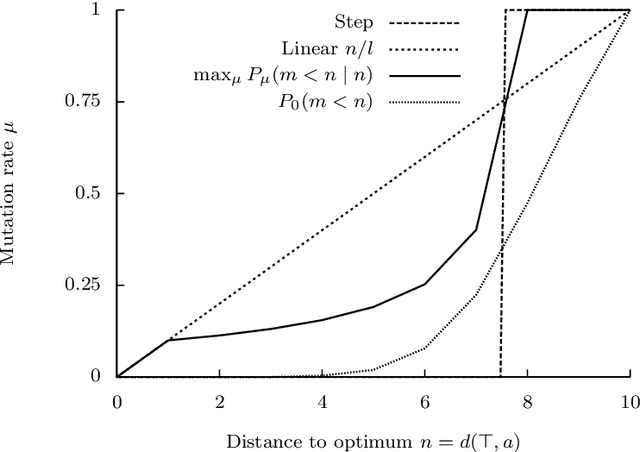
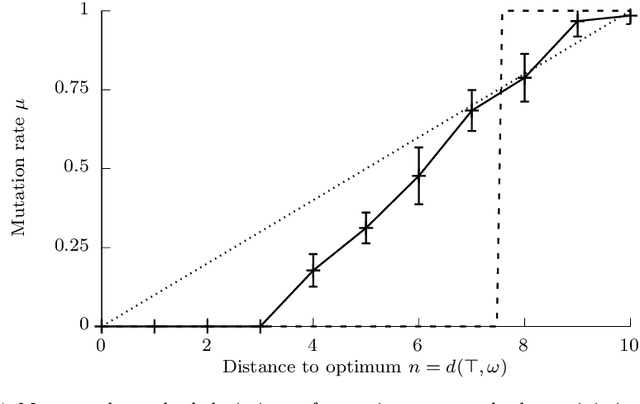
The typical view in evolutionary biology is that mutation rates are minimised. Contrary to that view, studies in combinatorial optimisation and search have shown a clear advantage of using variable mutation rates as a control parameter to optimise the performance of evolutionary algorithms. Ronald Fisher's work is the basis of much biological theory in this area. He used Euclidean geometry of continuous, infinite phenotypic spaces to study the relation between mutation size and expected fitness of the offspring. Here we develop a general theory of optimal mutation rate control that is based on the alternative geometry of discrete and finite spaces of DNA sequences. We define the monotonic properties of fitness landscapes, which allows us to relate fitness to the topology of genotypes and mutation size. First, we consider the case of a perfectly monotonic fitness landscape, in which the optimal mutation rate control functions can be derived exactly or approximately depending on additional constraints of the problem. Then we consider the general case of non-monotonic landscapes. We use the ideas of local and weak monotonicity to show that optimal mutation rate control functions exist in any such landscape and that they resemble control functions in a monotonic landscape at least in some neighbourhood of a fitness maximum. Generally, optimal mutation rates increase when fitness decreases, and the increase of mutation rate is more rapid in landscapes that are less monotonic (more rugged). We demonstrate these relationships by obtaining and analysing approximately optimal mutation rate control functions in 115 complete landscapes of binding scores between DNA sequences and transcription factors. We discuss the relevance of these findings to living organisms, including the phenomenon of stress-induced mutagenesis.

Conservation Law of Utility and Equilibria in Non-Zero Sum Games

This short note demonstrates how one can define a transformation of a non-zero sum game into a zero sum, so that the optimal mixed strategy achieving equilibrium always exists. The transformation is equivalent to introduction of a passive player into a game (a player with a singleton set of pure strategies), whose payoff depends on the actions of the active players, and it is justified by the law of conservation of utility in a game. In a transformed game, each participant plays against all other players, including the passive player. The advantage of this approach is that the transformed game is zero-sum and has an equilibrium solution. The optimal strategy and the value of the new game, however, can be different from strategies that are rational in the original game. We demonstrate the principle using the Prisoner's Dilemma example.