Partially factorized variational inference for high-dimensional mixed models

While generalized linear mixed models (GLMMs) are a fundamental tool in applied statistics, many specifications -- such as those involving categorical factors with many levels or interaction terms -- can be computationally challenging to estimate due to the need to compute or approximate high-dimensional integrals. Variational inference (VI) methods are a popular way to perform such computations, especially in the Bayesian context. However, naive VI methods can provide unreliable uncertainty quantification. We show that this is indeed the case in the GLMM context, proving that standard VI (i.e. mean-field) dramatically underestimates posterior uncertainty in high-dimensions. We then show how appropriately relaxing the mean-field assumption leads to VI methods whose uncertainty quantification does not deteriorate in high-dimensions, and whose total computational cost scales linearly with the number of parameters and observations. Our theoretical and numerical results focus on GLMMs with Gaussian or binomial likelihoods, and rely on connections to random graph theory to obtain sharp high-dimensional asymptotic analysis. We also provide generic results, which are of independent interest, relating the accuracy of variational inference to the convergence rate of the corresponding coordinate ascent variational inference (CAVI) algorithm for Gaussian targets. Our proposed partially-factorized VI (PF-VI) methodology for GLMMs is implemented in the R package vglmer, see https://github.com/mgoplerud/vglmer . Numerical results with simulated and real data examples illustrate the favourable computation cost versus accuracy trade-off of PF-VI.

Generalized Kernel Regularized Least Squares

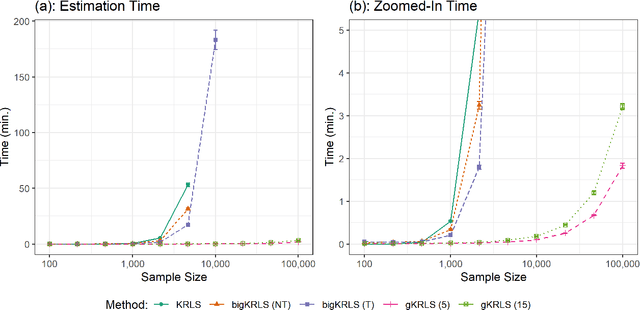
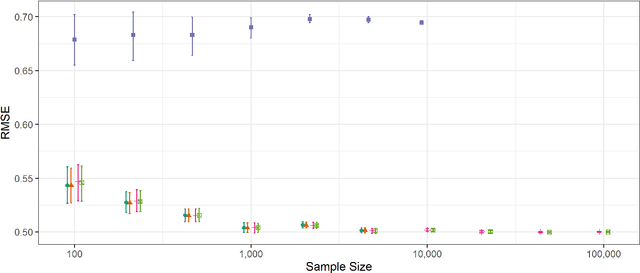
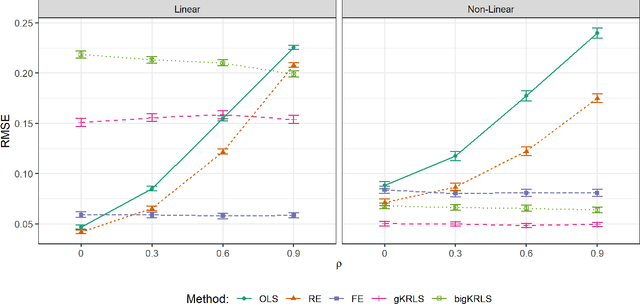
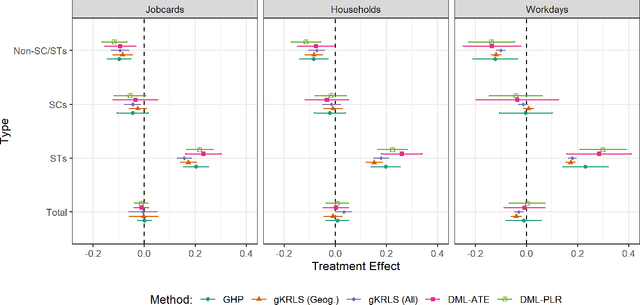
Kernel Regularized Least Squares (KRLS) is a popular method for flexibly estimating models that may have complex relationships between variables. However, its usefulness to many researchers is limited for two reasons. First, existing approaches are inflexible and do not allow KRLS to be combined with theoretically-motivated extensions such as fixed effects or non-linear outcomes. Second, estimation is extremely computationally intensive for even modestly sized datasets. Our paper addresses both concerns by introducing generalized KRLS (gKRLS). We note that KRLS can be re-formulated as a hierarchical model thereby allowing easy inference and modular model construction. Computationally, we also implement random sketching to dramatically accelerate estimation while incurring a limited penalty in estimation quality. We demonstrate that gKRLS can be fit on datasets with tens of thousands of observations in under one minute. Further, state-of-the-art techniques that require fitting the model over a dozen times (e.g. meta-learners) can be estimated quickly.

Modelling Heterogeneity Using Bayesian Structured Sparsity

How to estimate heterogeneity, e.g. the effect of some variable differing across observations, is a key question in political science. Methods for doing so make simplifying assumptions about the underlying nature of the heterogeneity to draw reliable inferences. This paper allows a common way of simplifying complex phenomenon (placing observations with similar effects into discrete groups) to be integrated into regression analysis. The framework allows researchers to (i) use their prior knowledge to guide which groups are permissible and (ii) appropriately quantify uncertainty. The paper does this by extending work on "structured sparsity" from a traditional penalized likelihood approach to a Bayesian one by deriving new theoretical results and inferential techniques. It shows that this method outperforms state-of-the-art methods for estimating heterogeneous effects when the underlying heterogeneity is grouped and more effectively identifies groups of observations with different effects in observational data.