d-blink: Distributed End-to-End Bayesian Entity Resolution

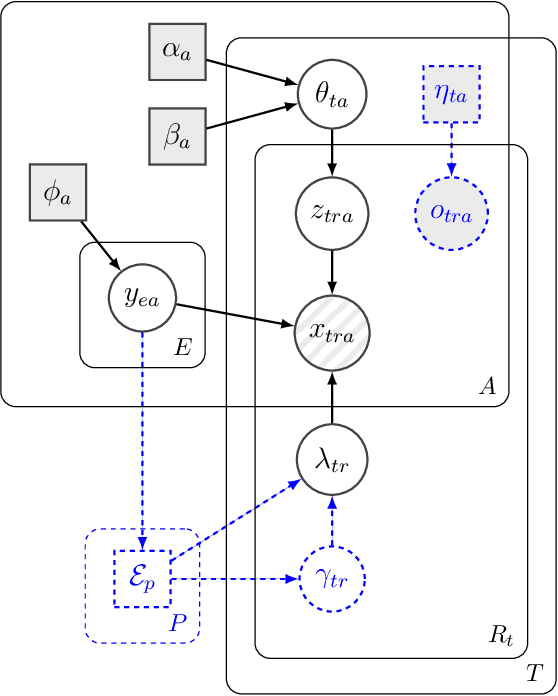
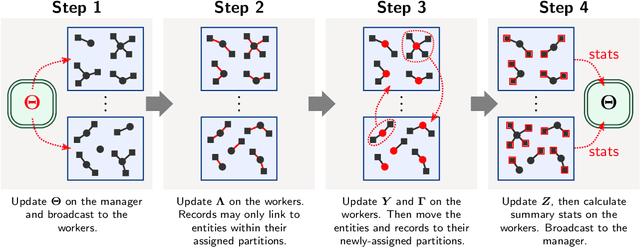
Entity resolution (ER) (record linkage or de-duplication) is the process of merging together noisy databases, often in the absence of a unique identifier. A major advancement in ER methodology has been the application of Bayesian generative models. Such models provide a natural framework for clustering records to unobserved (latent) entities, while providing exact uncertainty quantification and tight performance bounds. Despite these advancements, existing models do not scale to realistically-sized databases (larger than 1000 records) and they do not incorporate probabilistic blocking. In this paper, we propose "distributed Bayesian linkage" or d-blink -- the first scalable and distributed end-to-end Bayesian model for ER, which propagates uncertainty in blocking, matching and merging. We make several novel contributions, including: (i) incorporating probabilistic blocking directly into the model through auxiliary partitions; (ii) support for missing values; (iii) a partially-collapsed Gibbs sampler; and (iv) a novel perturbation sampling algorithm (leveraging the Vose-Alias method) that enables fast updates of the entity attributes. Finally, we conduct experiments on five data sets which show that d-blink can achieve significant efficiency gains -- in excess of 300$\times$ -- when compared to existing non-distributed methods.

Posterior Prototyping: Bridging the Gap between Bayesian Record Linkage and Regression

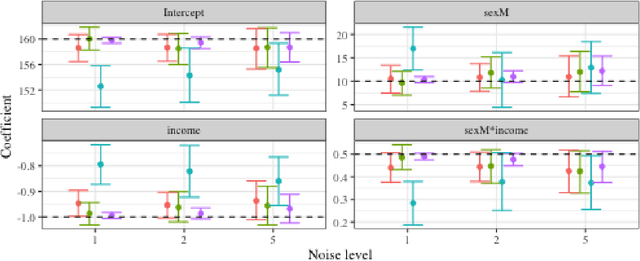
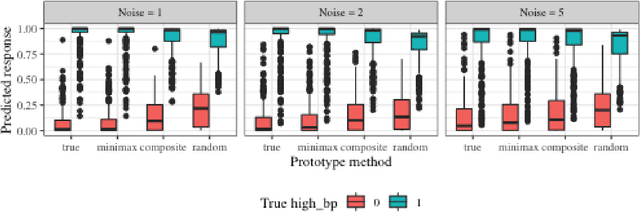
Record linkage (entity resolution or de-deduplication) is the process of merging noisy databases to remove duplicate entities. While record linkage removes duplicate entities from the data, many researchers are interested in performing inference, prediction or post-linkage analysis on the linked data, which we call the downstream task. Depending on the downstream task, one may wish to find the most representative record before performing the post-linkage analysis. Motivated by the downstream task, we propose first performing record linkage using a Bayesian model and then choosing representative records through prototyping. Given the information about the representative records, we then explore two downstream tasks - linear regression and binary classification via logistic regression. In addition, we explore how error propagation occurs in both of these settings. We provide thorough empirical studies for our proposed methodology, and conclude with a discussion of practical insights into our work.

Properties and Bayesian fitting of restricted Boltzmann machines

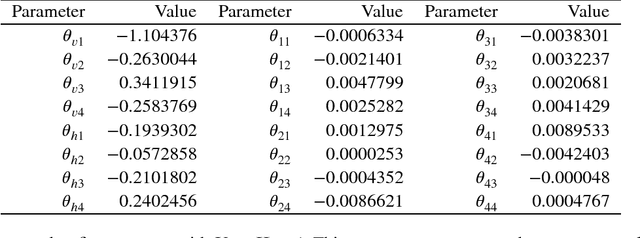
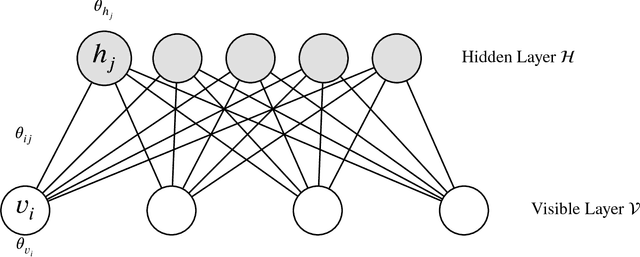
A restricted Boltzmann machine (RBM) is an undirected graphical model constructed for discrete or continuous random variables, with two layers, one hidden and one visible, and no conditional dependency within a layer. In recent years, RBMs have risen to prominence due to their connection to deep learning. By treating a hidden layer of one RBM as the visible layer in a second RBM, a deep architecture can be created. RBMs are thought to thereby have the ability to encode very complex and rich structures in data, making them attractive for supervised learning. However, the generative behavior of RBMs is largely unexplored and typical fitting methodology does not easily allow for uncertainty quantification in addition to point estimates. In this paper, we discuss the relationship between RBM parameter specification in the binary case and model properties such as degeneracy, instability and uninterpretability. We also describe the associated difficulties that can arise with likelihood-based inference and further discuss the potential Bayes fitting of such (highly flexible) models, especially as Gibbs sampling (quasi-Bayes) methods are often advocated for the RBM model structure.