Discovering group dynamics in synchronous time series via hierarchical recurrent switching-state models

We seek to model a collection of time series arising from multiple entities interacting over the same time period. Recent work focused on modeling individual time series is inadequate for our intended applications, where collective system-level behavior influences the trajectories of individual entities. To address such problems, we present a new hierarchical switching-state model that can be trained in an unsupervised fashion to simultaneously explain both system-level and individual-level dynamics. We employ a latent system-level discrete state Markov chain that drives latent entity-level chains which in turn govern the dynamics of each observed time series. Feedback from the observations to the chains at both the entity and system levels improves flexibility via context-dependent state transitions. Our hierarchical switching recurrent dynamical models can be learned via closed-form variational coordinate ascent updates to all latent chains that scale linearly in the number of individual time series. This is asymptotically no more costly than fitting separate models for each entity. Experiments on synthetic and real datasets show that our model can produce better forecasts of future entity behavior than existing methods. Moreover, the availability of latent state chains at both the entity and system level enables interpretation of group dynamics.

Projecting "better than randomly": How to reduce the dimensionality of very large datasets in a way that outperforms random projections

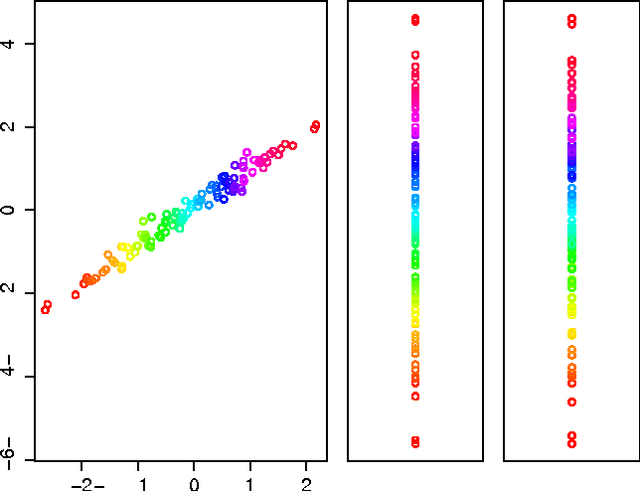
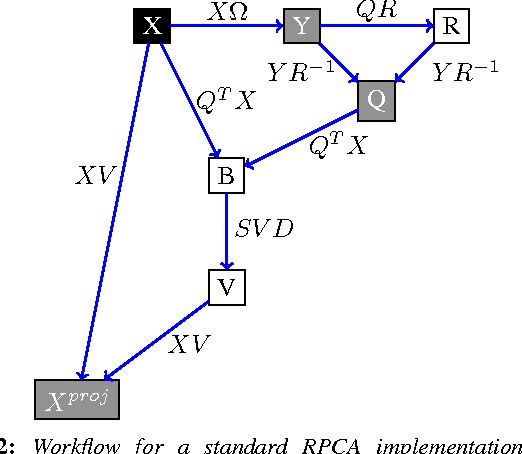
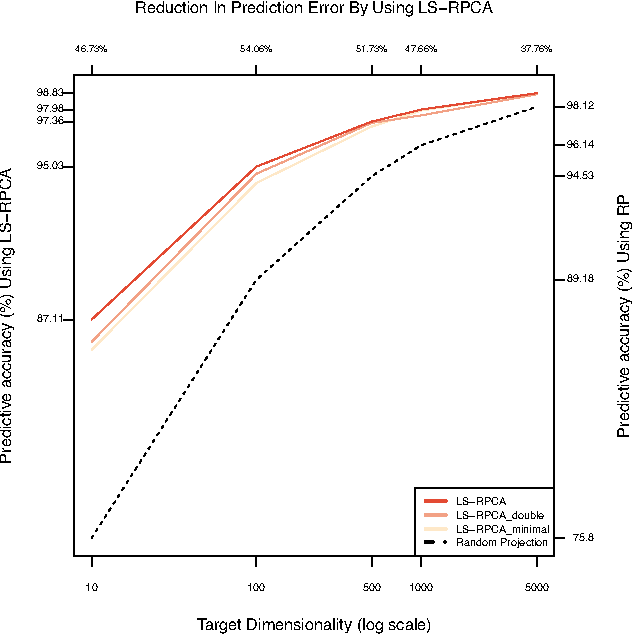
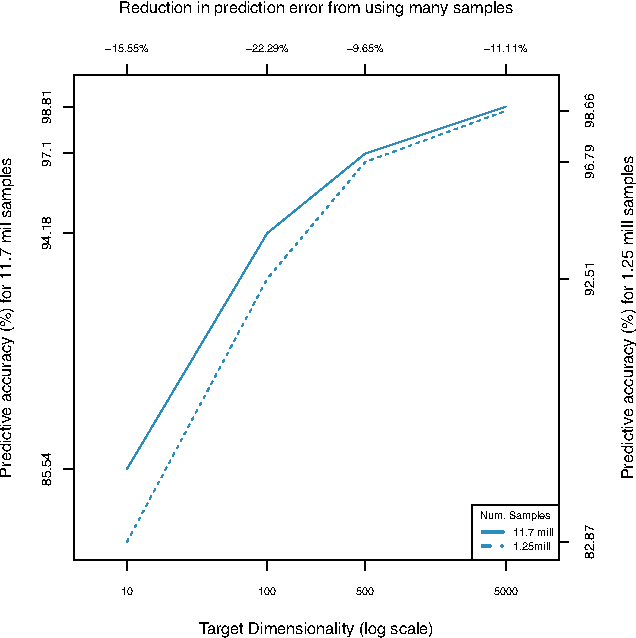
For very large datasets, random projections (RP) have become the tool of choice for dimensionality reduction. This is due to the computational complexity of principal component analysis. However, the recent development of randomized principal component analysis (RPCA) has opened up the possibility of obtaining approximate principal components on very large datasets. In this paper, we compare the performance of RPCA and RP in dimensionality reduction for supervised learning. In Experiment 1, study a malware classification task on a dataset with over 10 million samples, almost 100,000 features, and over 25 billion non-zero values, with the goal of reducing the dimensionality to a compressed representation of 5,000 features. In order to apply RPCA to this dataset, we develop a new algorithm called large sample RPCA (LS-RPCA), which extends the RPCA algorithm to work on datasets with arbitrarily many samples. We find that classification performance is much higher when using LS-RPCA for dimensionality reduction than when using random projections. In particular, across a range of target dimensionalities, we find that using LS-RPCA reduces classification error by between 37% and 54%. Experiment 2 generalizes the phenomenon to multiple datasets, feature representations, and classifiers. These findings have implications for a large number of research projects in which random projections were used as a preprocessing step for dimensionality reduction. As long as accuracy is at a premium and the target dimensionality is sufficiently less than the numeric rank of the dataset, randomized PCA may be a superior choice. Moreover, if the dataset has a large number of samples, then LS-RPCA will provide a method for obtaining the approximate principal components.

Lazy stochastic principal component analysis

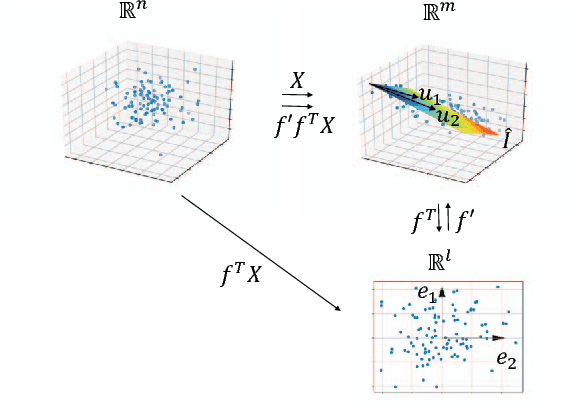
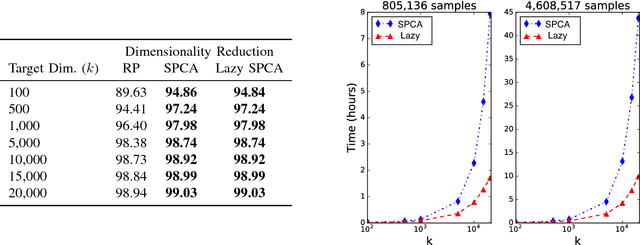
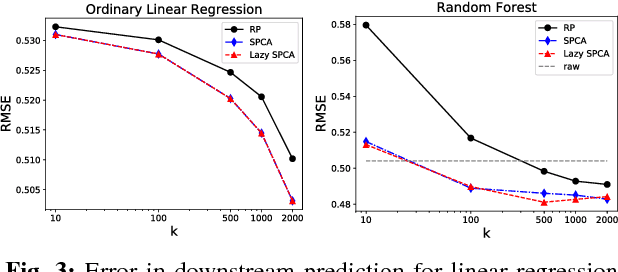
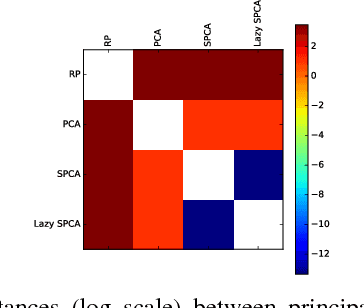
Stochastic principal component analysis (SPCA) has become a popular dimensionality reduction strategy for large, high-dimensional datasets. We derive a simplified algorithm, called Lazy SPCA, which has reduced computational complexity and is better suited for large-scale distributed computation. We prove that SPCA and Lazy SPCA find the same approximations to the principal subspace, and that the pairwise distances between samples in the lower-dimensional space is invariant to whether SPCA is executed lazily or not. Empirical studies find downstream predictive performance to be identical for both methods, and superior to random projections, across a range of predictive models (linear regression, logistic lasso, and random forests). In our largest experiment with 4.6 million samples, Lazy SPCA reduced 43.7 hours of computation to 9.9 hours. Overall, Lazy SPCA relies exclusively on matrix multiplications, besides an operation on a small square matrix whose size depends only on the target dimensionality.