Projecting "better than randomly": How to reduce the dimensionality of very large datasets in a way that outperforms random projections

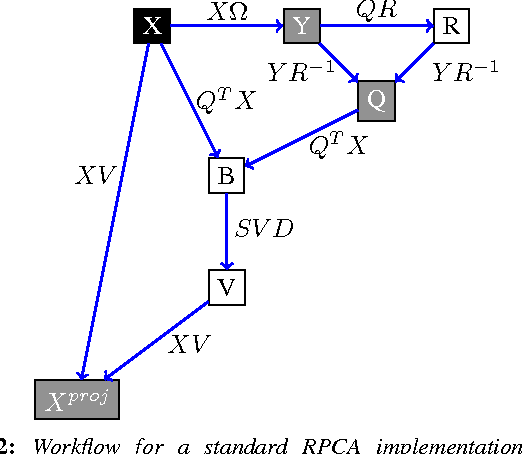
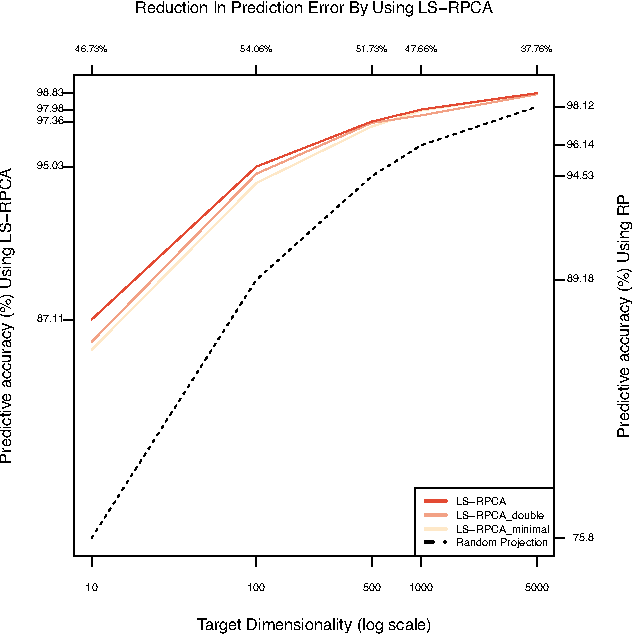
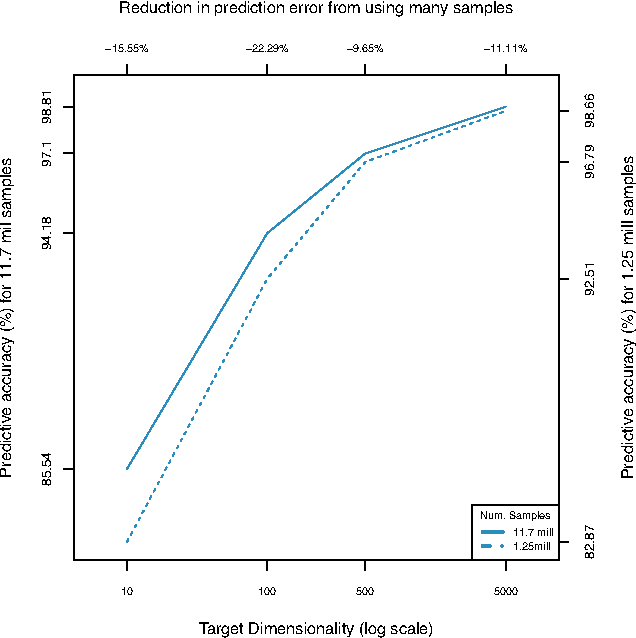
For very large datasets, random projections (RP) have become the tool of choice for dimensionality reduction. This is due to the computational complexity of principal component analysis. However, the recent development of randomized principal component analysis (RPCA) has opened up the possibility of obtaining approximate principal components on very large datasets. In this paper, we compare the performance of RPCA and RP in dimensionality reduction for supervised learning. In Experiment 1, study a malware classification task on a dataset with over 10 million samples, almost 100,000 features, and over 25 billion non-zero values, with the goal of reducing the dimensionality to a compressed representation of 5,000 features. In order to apply RPCA to this dataset, we develop a new algorithm called large sample RPCA (LS-RPCA), which extends the RPCA algorithm to work on datasets with arbitrarily many samples. We find that classification performance is much higher when using LS-RPCA for dimensionality reduction than when using random projections. In particular, across a range of target dimensionalities, we find that using LS-RPCA reduces classification error by between 37% and 54%. Experiment 2 generalizes the phenomenon to multiple datasets, feature representations, and classifiers. These findings have implications for a large number of research projects in which random projections were used as a preprocessing step for dimensionality reduction. As long as accuracy is at a premium and the target dimensionality is sufficiently less than the numeric rank of the dataset, randomized PCA may be a superior choice. Moreover, if the dataset has a large number of samples, then LS-RPCA will provide a method for obtaining the approximate principal components.

"Influence Sketching": Finding Influential Samples In Large-Scale Regressions

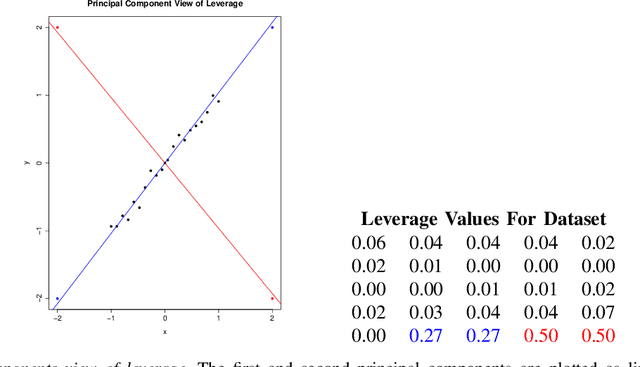
There is an especially strong need in modern large-scale data analysis to prioritize samples for manual inspection. For example, the inspection could target important mislabeled samples or key vulnerabilities exploitable by an adversarial attack. In order to solve the "needle in the haystack" problem of which samples to inspect, we develop a new scalable version of Cook's distance, a classical statistical technique for identifying samples which unusually strongly impact the fit of a regression model (and its downstream predictions). In order to scale this technique up to very large and high-dimensional datasets, we introduce a new algorithm which we call "influence sketching." Influence sketching embeds random projections within the influence computation; in particular, the influence score is calculated using the randomly projected pseudo-dataset from the post-convergence Generalized Linear Model (GLM). We validate that influence sketching can reliably and successfully discover influential samples by applying the technique to a malware detection dataset of over 2 million executable files, each represented with almost 100,000 features. For example, we find that randomly deleting approximately 10% of training samples reduces predictive accuracy only slightly from 99.47% to 99.45%, whereas deleting the same number of samples with high influence sketch scores reduces predictive accuracy all the way down to 90.24%. Moreover, we find that influential samples are especially likely to be mislabeled. In the case study, we manually inspect the most influential samples, and find that influence sketching pointed us to new, previously unidentified pieces of malware.