Lazy stochastic principal component analysis
Paper and Code
Sep 21, 2017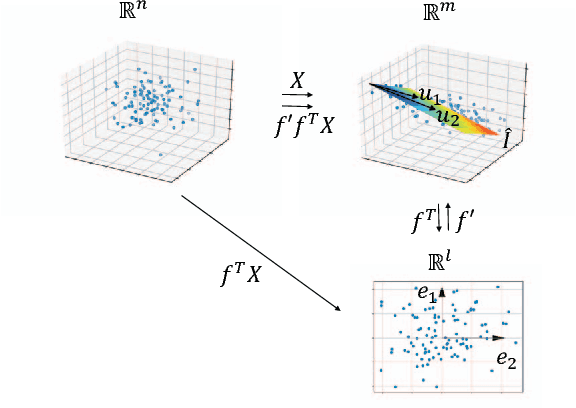
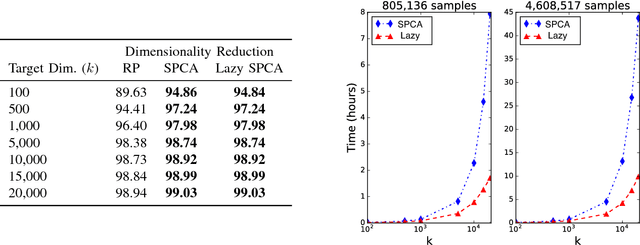
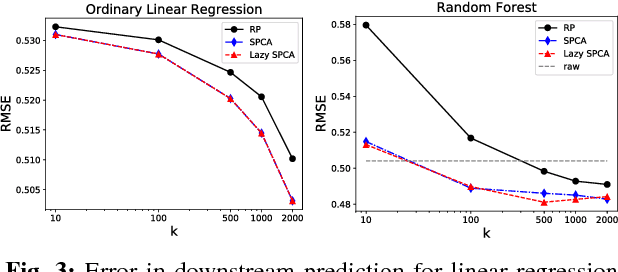
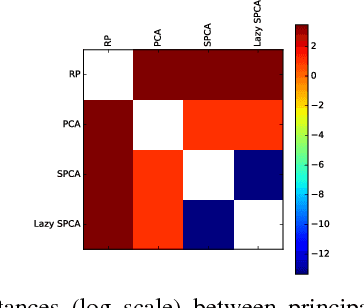
Stochastic principal component analysis (SPCA) has become a popular dimensionality reduction strategy for large, high-dimensional datasets. We derive a simplified algorithm, called Lazy SPCA, which has reduced computational complexity and is better suited for large-scale distributed computation. We prove that SPCA and Lazy SPCA find the same approximations to the principal subspace, and that the pairwise distances between samples in the lower-dimensional space is invariant to whether SPCA is executed lazily or not. Empirical studies find downstream predictive performance to be identical for both methods, and superior to random projections, across a range of predictive models (linear regression, logistic lasso, and random forests). In our largest experiment with 4.6 million samples, Lazy SPCA reduced 43.7 hours of computation to 9.9 hours. Overall, Lazy SPCA relies exclusively on matrix multiplications, besides an operation on a small square matrix whose size depends only on the target dimensionality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge