Non-Parametric and Regularized Dynamical Wasserstein Barycenters for Time-Series Analysis

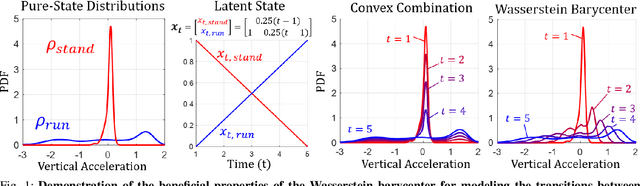
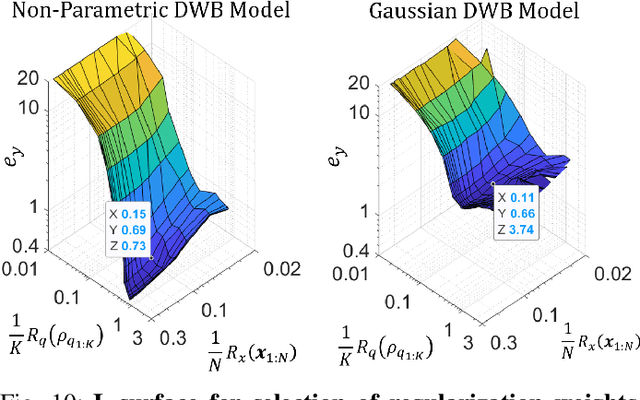
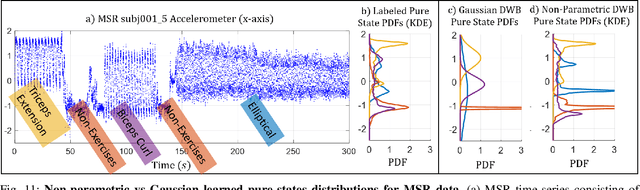
We consider probabilistic time-series models for systems that gradually transition among a finite number of states. We are particularly motivated by applications such as human activity analysis where the observed time-series contains segments representing distinct activities such as running or walking as well as segments characterized by continuous transition among these states. Accordingly, the dynamical Wasserstein barycenter (DWB) model introduced in Cheng et al. in 2021 [1] associates with each state, which we call a pure state, its own probability distribution, and models these continuous transitions with the dynamics of the barycentric weights that combine the pure state distributions via the Wasserstein barycenter. Here, focusing on the univariate case where Wasserstein distances and barycenters can be computed in closed form, we extend [1] by discussing two challenges associated with learning a DWB model and two improvements. First, we highlight the issue of uniqueness in identifying the model parameters. Secondly, we discuss the challenge of estimating a dynamically evolving distribution given a limited number of samples. The uncertainty associated with this estimation may cause a model's learned dynamics to not reflect the gradual transitions characteristic of the system. The first improvement introduces a regularization framework that addresses this uncertainty by imposing temporal smoothness on the dynamics of the barycentric weights while leveraging the understanding of the non-uniqueness of the problem. This is done without defining an entire stochastic model for the dynamics of the system as in [1]. Our second improvement lifts the Gaussian assumption on the pure states distributions in [1] by proposing a quantile-based non-parametric representation. We pose model estimation in a variational framework and propose a finite approximation to the infinite dimensional problem.

Dynamical Wasserstein Barycenters for Time-series Modeling

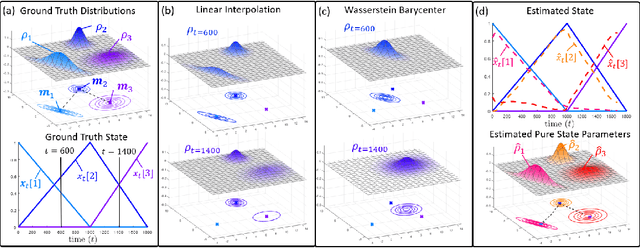
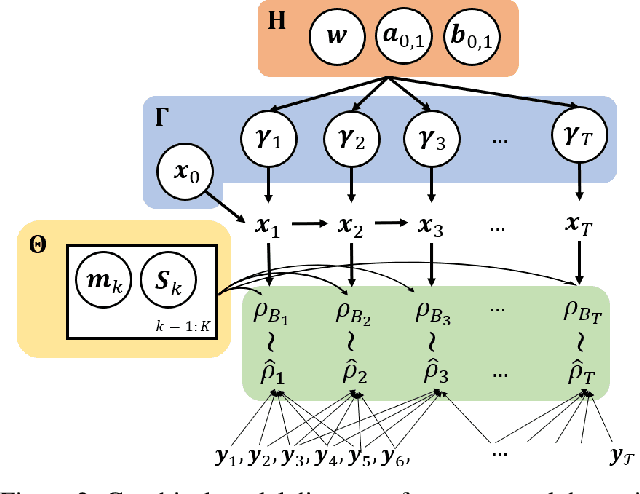
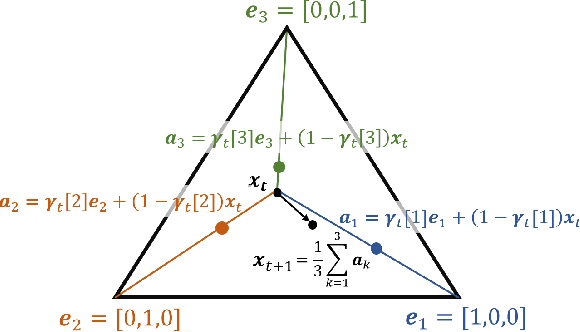
Many time series can be modeled as a sequence of segments representing high-level discrete states, such as running and walking in a human activity application. Flexible models should describe the system state and observations in stationary "pure-state" periods as well as transition periods between adjacent segments, such as a gradual slowdown between running and walking. However, most prior work assumes instantaneous transitions between pure discrete states. We propose a dynamical Wasserstein barycentric (DWB) model that estimates the system state over time as well as the data-generating distributions of pure states in an unsupervised manner. Our model assumes each pure state generates data from a multivariate normal distribution, and characterizes transitions between states via displacement-interpolation specified by the Wasserstein barycenter. The system state is represented by a barycentric weight vector which evolves over time via a random walk on the simplex. Parameter learning leverages the natural Riemannian geometry of Gaussian distributions under the Wasserstein distance, which leads to improved convergence speeds. Experiments on several human activity datasets show that our proposed DWB model accurately learns the generating distribution of pure states while improving state estimation for transition periods compared to the commonly used linear interpolation mixture models.

On Matched Filtering for Statistical Change Point Detection

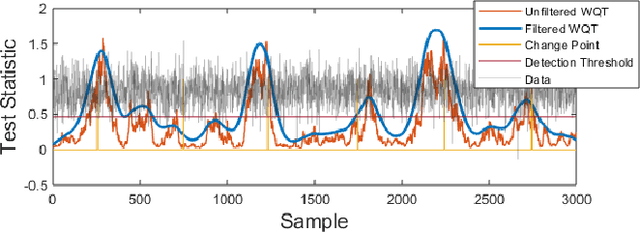
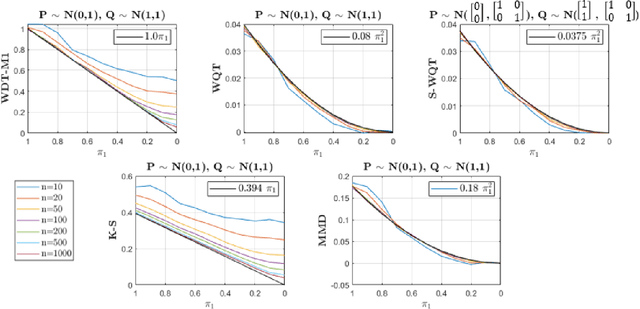
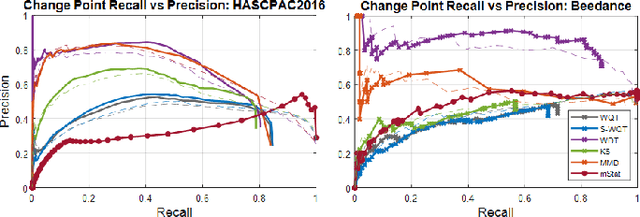
Non-parametric and distribution-free two-sample tests have been the foundation of many change point detection algorithms.However, noise in the data make these tests susceptible to false positives and localization ambiguity. We address these issues by deriving asymptotically matched filters under standard IID assumptions on the data for various sliding window two-sample tests.In particular, in this paper we focus on the Wasserstein quantile test, the Wasserstein-1 distance test, maximum mean discrepancy(MMD) test, and the Kolmogorov-Smirnov (KS) test. To the best of our knowledge this is the first time an matched filtering has been proposed and evaluated for these tests or for change point detection. While in this paper we only consider a subset of tests, the proposed methodology and analysis can be extended to other tests. Quite remarkably, this simple post processing turns out to be quite robust in terms of mitigating false positives and improving change point localization, thereby making these distribution-free tests practically useful. We demonstrate this through experiments on synthetic data as well as activity recognition benchmarks. We further highlight and contrast several properties such as sensitivity of these tests and compare their relative performance.

Optimal Transport Based Change Point Detection and Time Series Segment Clustering

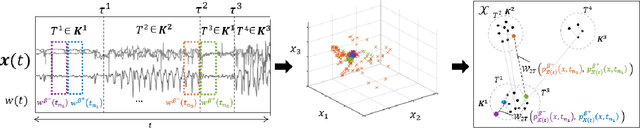
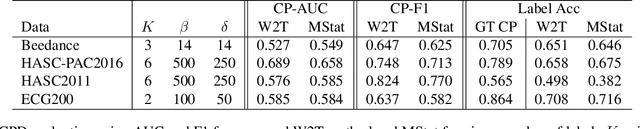
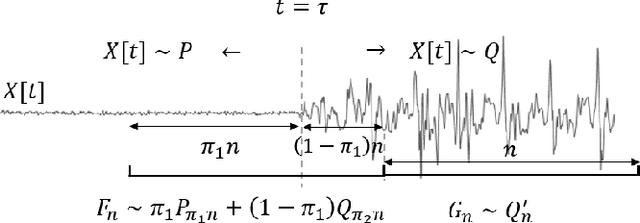
Two common problems in time series analysis are the decomposition of the data stream into disjoint segments, each of which is in some sense 'homogeneous' - a problem that is also referred to as Change Point Detection (CPD) - and the grouping of similar nonadjacent segments, or Time Series Segment Clustering (TSSC). Building upon recent theoretical advances characterizing the limiting distribution free behavior of the Wasserstein two-sample test, we propose a novel algorithm for unsupervised, distribution-free CPD, which is amenable to both offline and online settings. We also introduce a method to mitigate false positives in CPD, and address TSSC by using the Wasserstein distance between the detected segments to build an affinity matrix to which we apply spectral clustering. Results on both synthetic and real data sets show the benefits of the approach.