Non-Parametric and Regularized Dynamical Wasserstein Barycenters for Time-Series Analysis

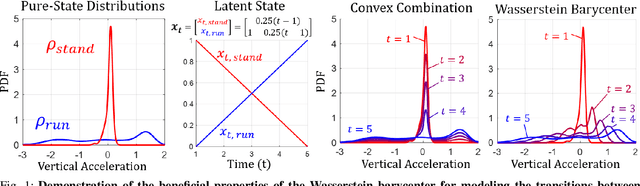
We consider probabilistic time-series models for systems that gradually transition among a finite number of states. We are particularly motivated by applications such as human activity analysis where the observed time-series contains segments representing distinct activities such as running or walking as well as segments characterized by continuous transition among these states. Accordingly, the dynamical Wasserstein barycenter (DWB) model introduced in Cheng et al. in 2021 [1] associates with each state, which we call a pure state, its own probability distribution, and models these continuous transitions with the dynamics of the barycentric weights that combine the pure state distributions via the Wasserstein barycenter. Here, focusing on the univariate case where Wasserstein distances and barycenters can be computed in closed form, we extend [1] by discussing two challenges associated with learning a DWB model and two improvements. First, we highlight the issue of uniqueness in identifying the model parameters. Secondly, we discuss the challenge of estimating a dynamically evolving distribution given a limited number of samples. The uncertainty associated with this estimation may cause a model's learned dynamics to not reflect the gradual transitions characteristic of the system. The first improvement introduces a regularization framework that addresses this uncertainty by imposing temporal smoothness on the dynamics of the barycentric weights while leveraging the understanding of the non-uniqueness of the problem. This is done without defining an entire stochastic model for the dynamics of the system as in [1]. Our second improvement lifts the Gaussian assumption on the pure states distributions in [1] by proposing a quantile-based non-parametric representation. We pose model estimation in a variational framework and propose a finite approximation to the infinite dimensional problem.