Dynamical Wasserstein Barycenters for Time-series Modeling
Paper and Code
Oct 29, 2021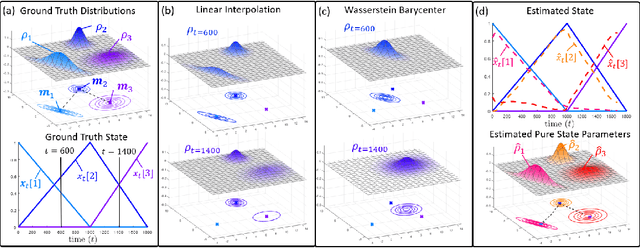
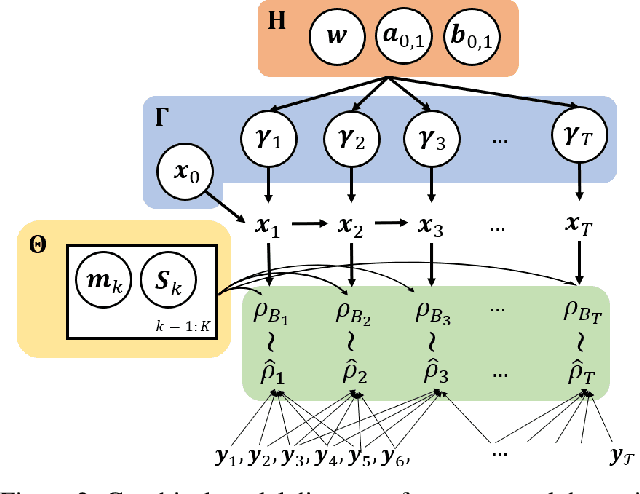
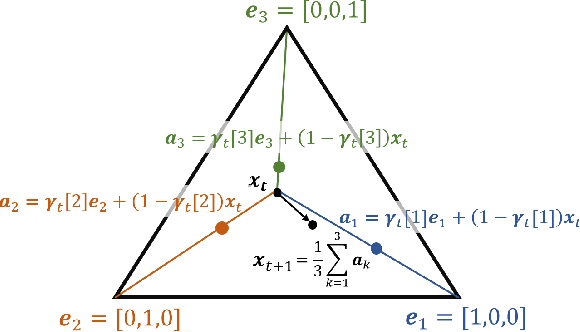

Many time series can be modeled as a sequence of segments representing high-level discrete states, such as running and walking in a human activity application. Flexible models should describe the system state and observations in stationary "pure-state" periods as well as transition periods between adjacent segments, such as a gradual slowdown between running and walking. However, most prior work assumes instantaneous transitions between pure discrete states. We propose a dynamical Wasserstein barycentric (DWB) model that estimates the system state over time as well as the data-generating distributions of pure states in an unsupervised manner. Our model assumes each pure state generates data from a multivariate normal distribution, and characterizes transitions between states via displacement-interpolation specified by the Wasserstein barycenter. The system state is represented by a barycentric weight vector which evolves over time via a random walk on the simplex. Parameter learning leverages the natural Riemannian geometry of Gaussian distributions under the Wasserstein distance, which leads to improved convergence speeds. Experiments on several human activity datasets show that our proposed DWB model accurately learns the generating distribution of pure states while improving state estimation for transition periods compared to the commonly used linear interpolation mixture models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge