On Matched Filtering for Statistical Change Point Detection
Paper and Code
Jun 09, 2020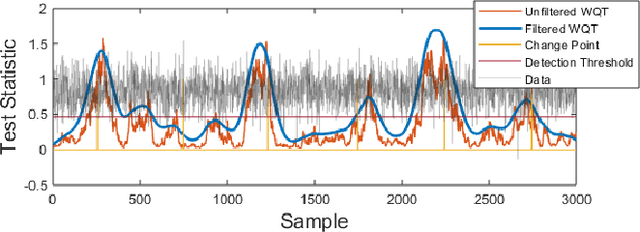
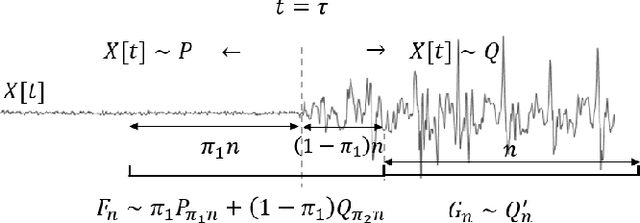
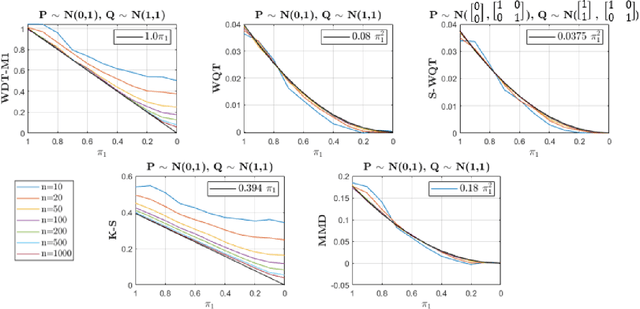
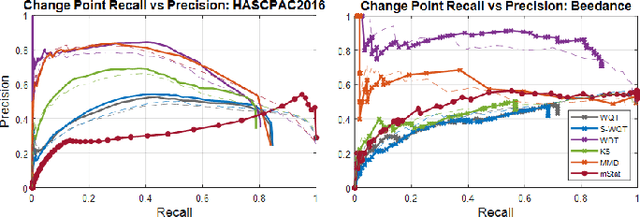
Non-parametric and distribution-free two-sample tests have been the foundation of many change point detection algorithms.However, noise in the data make these tests susceptible to false positives and localization ambiguity. We address these issues by deriving asymptotically matched filters under standard IID assumptions on the data for various sliding window two-sample tests.In particular, in this paper we focus on the Wasserstein quantile test, the Wasserstein-1 distance test, maximum mean discrepancy(MMD) test, and the Kolmogorov-Smirnov (KS) test. To the best of our knowledge this is the first time an matched filtering has been proposed and evaluated for these tests or for change point detection. While in this paper we only consider a subset of tests, the proposed methodology and analysis can be extended to other tests. Quite remarkably, this simple post processing turns out to be quite robust in terms of mitigating false positives and improving change point localization, thereby making these distribution-free tests practically useful. We demonstrate this through experiments on synthetic data as well as activity recognition benchmarks. We further highlight and contrast several properties such as sensitivity of these tests and compare their relative performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge