A Parametric Level Set Approach to Simultaneous Object Identification and Background Reconstruction for Dual Energy Computed Tomography
Paper and Code
Mar 29, 2011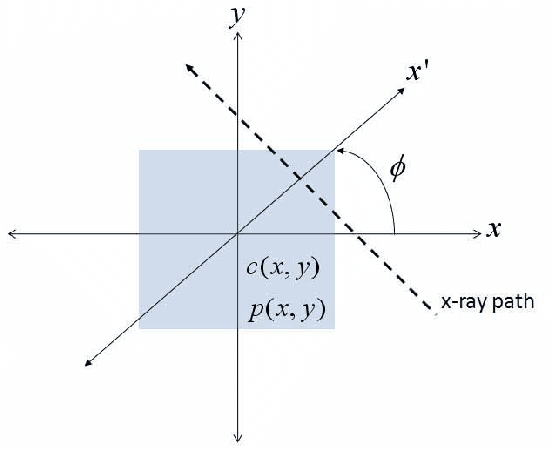
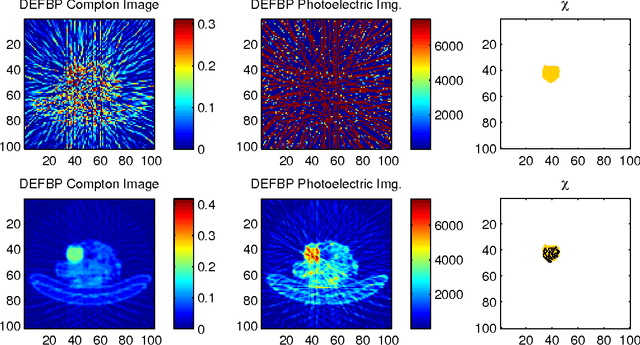
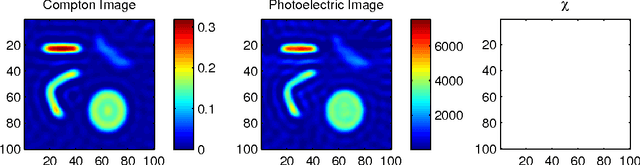
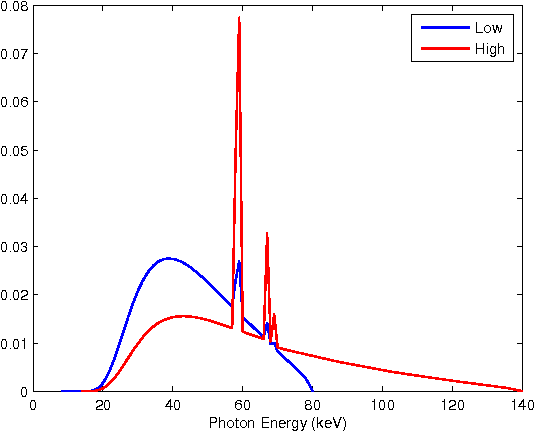
Dual energy computerized tomography has gained great interest because of its ability to characterize the chemical composition of a material rather than simply providing relative attenuation images as in conventional tomography. The purpose of this paper is to introduce a novel polychromatic dual energy processing algorithm with an emphasis on detection and characterization of piecewise constant objects embedded in an unknown, cluttered background. Physical properties of the objects, specifically the Compton scattering and photoelectric absorption coefficients, are assumed to be known with some level of uncertainty. Our approach is based on a level-set representation of the characteristic function of the object and encompasses a number of regularization techniques for addressing both the prior information we have concerning the physical properties of the object as well as fundamental, physics-based limitations associated with our ability to jointly recover the Compton scattering and photoelectric absorption properties of the scene. In the absence of an object with appropriate physical properties, our approach returns a null characteristic function and thus can be viewed as simultaneously solving the detection and characterization problems. Unlike the vast majority of methods which define the level set function non-parametrically, i.e., as a dense set of pixel values), we define our level set parametrically via radial basis functions (RBF's) and employ a Gauss-Newton type algorithm for cost minimization. Numerical results show that the algorithm successfully detects objects of interest, finds their shape and location, and gives a adequate reconstruction of the background.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge