On Symbol Error Probability-based Beamforming in MIMO Gaussian Wiretap Channels

This paper investigates beamforming schemes designed to minimize the symbol error probability (SEP) for an authorized user while guaranteeing that the likelihood of an eavesdropper correctly recovering symbols remains below a predefined threshold. Unlike previous works that focus on maximizing secrecy capacity, our work is centered around finding an optimal beamforming vector for binary antipodal signal detection in multiple-input multiple-output (MIMO) Gaussian wiretap channels. Finding the optimal beamforming vector in this setting is challenging. Computationally efficient algorithms such as convex techniques cannot be applied to find the optimal solution. To that end, our proposed algorithm relies on Karush-Kuhn-Tucker (KKT) conditions and a generalized eigen-decomposition method to find the exact solution. In addition, we also develop an approximate, practical algorithm to find a good beamforming matrix when using M-ary detection schemes. Numerical results are presented to assess the performance of the proposed methods across various scenarios.

On neural and dimensional collapse in supervised and unsupervised contrastive learning with hard negative sampling

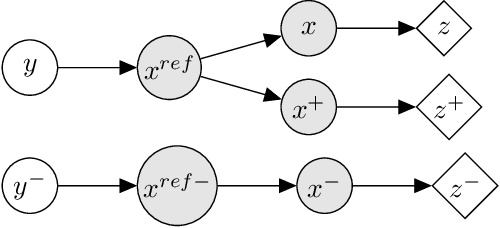
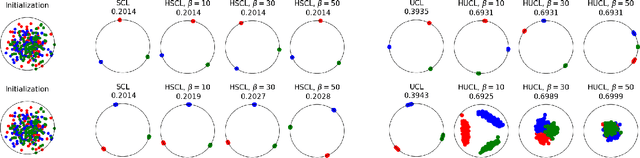
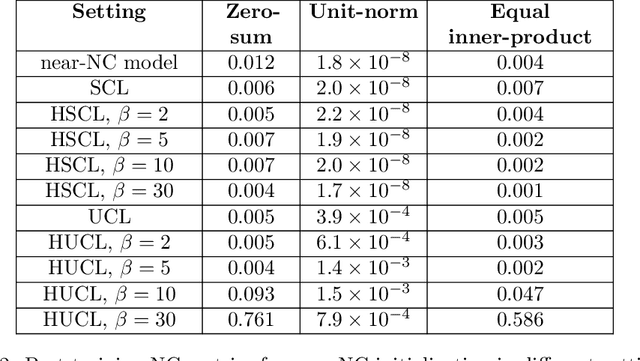
For a widely-studied data model and general loss and sample-hardening functions we prove that the Supervised Contrastive Learning (SCL), Hard-SCL (HSCL), and Unsupervised Contrastive Learning (UCL) risks are minimized by representations that exhibit Neural Collapse (NC), i.e., the class means form an Equianglular Tight Frame (ETF) and data from the same class are mapped to the same representation. We also prove that for any representation mapping, the HSCL and Hard-UCL (HUCL) risks are lower bounded by the corresponding SCL and UCL risks. Although the optimality of ETF is known for SCL, albeit only for InfoNCE loss, its optimality for HSCL and UCL under general loss and hardening functions is novel. Moreover, our proofs are much simpler, compact, and transparent. We empirically demonstrate, for the first time, that ADAM optimization of HSCL and HUCL risks with random initialization and suitable hardness levels can indeed converge to the NC geometry if we incorporate unit-ball or unit-sphere feature normalization. Without incorporating hard negatives or feature normalization, however, the representations learned via ADAM suffer from dimensional collapse (DC) and fail to attain the NC geometry.

A principled approach to model validation in domain generalization

Domain generalization aims to learn a model with good generalization ability, that is, the learned model should not only perform well on several seen domains but also on unseen domains with different data distributions. State-of-the-art domain generalization methods typically train a representation function followed by a classifier jointly to minimize both the classification risk and the domain discrepancy. However, when it comes to model selection, most of these methods rely on traditional validation routines that select models solely based on the lowest classification risk on the validation set. In this paper, we theoretically demonstrate a trade-off between minimizing classification risk and mitigating domain discrepancy, i.e., it is impossible to achieve the minimum of these two objectives simultaneously. Motivated by this theoretical result, we propose a novel model selection method suggesting that the validation process should account for both the classification risk and the domain discrepancy. We validate the effectiveness of the proposed method by numerical results on several domain generalization datasets.

Trade-off between reconstruction loss and feature alignment for domain generalization

Domain generalization (DG) is a branch of transfer learning that aims to train the learning models on several seen domains and subsequently apply these pre-trained models to other unseen (unknown but related) domains. To deal with challenging settings in DG where both data and label of the unseen domain are not available at training time, the most common approach is to design the classifiers based on the domain-invariant representation features, i.e., the latent representations that are unchanged and transferable between domains. Contrary to popular belief, we show that designing classifiers based on invariant representation features alone is necessary but insufficient in DG. Our analysis indicates the necessity of imposing a constraint on the reconstruction loss induced by representation functions to preserve most of the relevant information about the label in the latent space. More importantly, we point out the trade-off between minimizing the reconstruction loss and achieving domain alignment in DG. Our theoretical results motivate a new DG framework that jointly optimizes the reconstruction loss and the domain discrepancy. Both theoretical and numerical results are provided to justify our approach.

Joint covariate-alignment and concept-alignment: a framework for domain generalization

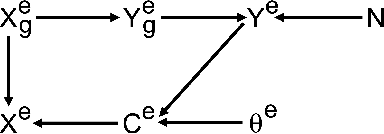
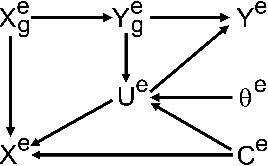
In this paper, we propose a novel domain generalization (DG) framework based on a new upper bound to the risk on the unseen domain. Particularly, our framework proposes to jointly minimize both the covariate-shift as well as the concept-shift between the seen domains for a better performance on the unseen domain. While the proposed approach can be implemented via an arbitrary combination of covariate-alignment and concept-alignment modules, in this work we use well-established approaches for distributional alignment namely, Maximum Mean Discrepancy (MMD) and covariance Alignment (CORAL), and use an Invariant Risk Minimization (IRM)-based approach for concept alignment. Our numerical results show that the proposed methods perform as well as or better than the state-of-the-art for domain generalization on several data sets.

Conditional entropy minimization principle for learning domain invariant representation features

Invariance principle-based methods, for example, Invariant Risk Minimization (IRM), have recently emerged as promising approaches for Domain Generalization (DG). Despite the promising theory, invariance principle-based approaches fail in common classification tasks due to the mixture of the true invariant features and the spurious invariant features. In this paper, we propose a framework based on the conditional entropy minimization principle to filter out the spurious invariant features leading to a new algorithm with a better generalization capability. We theoretically prove that under some particular assumptions, the representation function can precisely recover the true invariant features. In addition, we also show that the proposed approach is closely related to the well-known Information Bottleneck framework. Both the theoretical and numerical results are provided to justify our approach.

Barycenteric distribution alignment and manifold-restricted invertibility for domain generalization

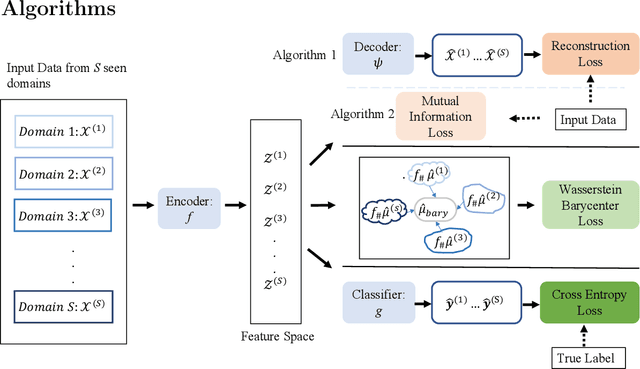
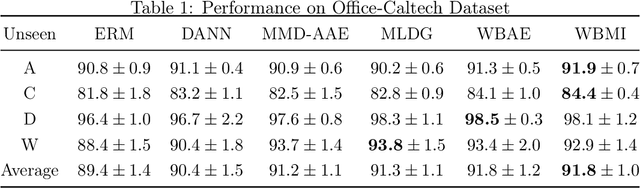
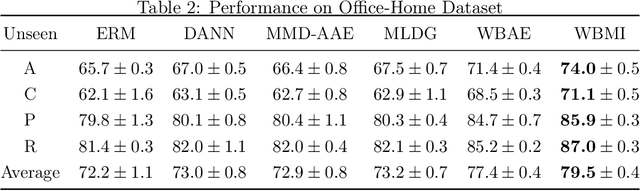
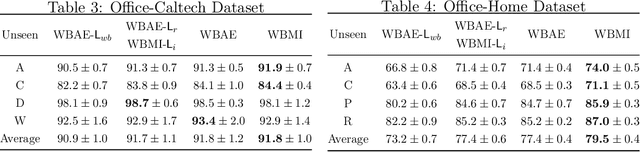
For the Domain Generalization (DG) problem where the hypotheses are composed of a common representation function followed by a labeling function, we point out a shortcoming in existing approaches that fail to explicitly optimize for a term, appearing in a well-known and widely adopted upper bound to the risk on the unseen domain, that is dependent on the representation to be learned. To this end, we first derive a novel upper bound to the prediction risk. We show that imposing a mild assumption on the representation to be learned, namely manifold restricted invertibility, is sufficient to deal with this issue. Further, unlike existing approaches, our novel upper bound doesn't require the assumption of Lipschitzness of the loss function. In addition, the distributional discrepancy in the representation space is handled via the Wasserstein-2 barycenter cost. In this context, we creatively leverage old and recent transport inequalities, which link various optimal transport metrics, in particular the $L^1$ distance (also known as the total variation distance) and the Wasserstein-2 distances, with the Kullback-Liebler divergence. These analyses and insights motivate a new representation learning cost for DG that additively balances three competing objectives: 1) minimizing classification error across seen domains via cross-entropy, 2) enforcing domain-invariance in the representation space via the Wasserstein-2 barycenter cost, and 3) promoting non-degenerate, nearly-invertible representation via one of two mechanisms, viz., an autoencoder-based reconstruction loss or a mutual information loss. It is to be noted that the proposed algorithms completely bypass the use of any adversarial training mechanism that is typical of many current domain generalization approaches. Simulation results on several standard datasets demonstrate superior performance compared to several well-known DG algorithms.