Barycenteric distribution alignment and manifold-restricted invertibility for domain generalization
Paper and Code
Sep 04, 2021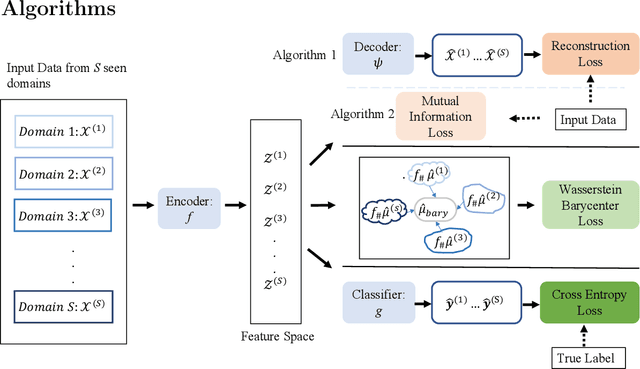
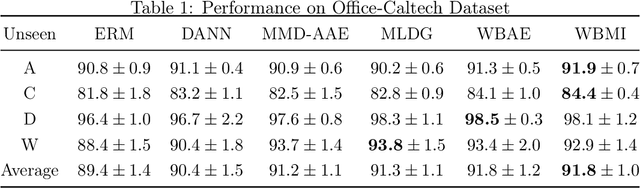
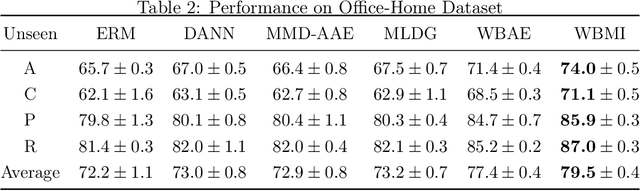
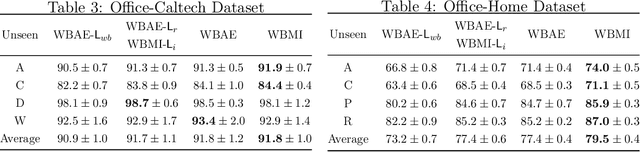
For the Domain Generalization (DG) problem where the hypotheses are composed of a common representation function followed by a labeling function, we point out a shortcoming in existing approaches that fail to explicitly optimize for a term, appearing in a well-known and widely adopted upper bound to the risk on the unseen domain, that is dependent on the representation to be learned. To this end, we first derive a novel upper bound to the prediction risk. We show that imposing a mild assumption on the representation to be learned, namely manifold restricted invertibility, is sufficient to deal with this issue. Further, unlike existing approaches, our novel upper bound doesn't require the assumption of Lipschitzness of the loss function. In addition, the distributional discrepancy in the representation space is handled via the Wasserstein-2 barycenter cost. In this context, we creatively leverage old and recent transport inequalities, which link various optimal transport metrics, in particular the $L^1$ distance (also known as the total variation distance) and the Wasserstein-2 distances, with the Kullback-Liebler divergence. These analyses and insights motivate a new representation learning cost for DG that additively balances three competing objectives: 1) minimizing classification error across seen domains via cross-entropy, 2) enforcing domain-invariance in the representation space via the Wasserstein-2 barycenter cost, and 3) promoting non-degenerate, nearly-invertible representation via one of two mechanisms, viz., an autoencoder-based reconstruction loss or a mutual information loss. It is to be noted that the proposed algorithms completely bypass the use of any adversarial training mechanism that is typical of many current domain generalization approaches. Simulation results on several standard datasets demonstrate superior performance compared to several well-known DG algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge