On neural and dimensional collapse in supervised and unsupervised contrastive learning with hard negative sampling
Paper and Code
Nov 09, 2023

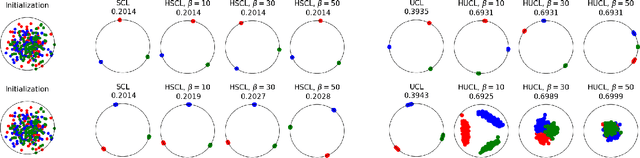
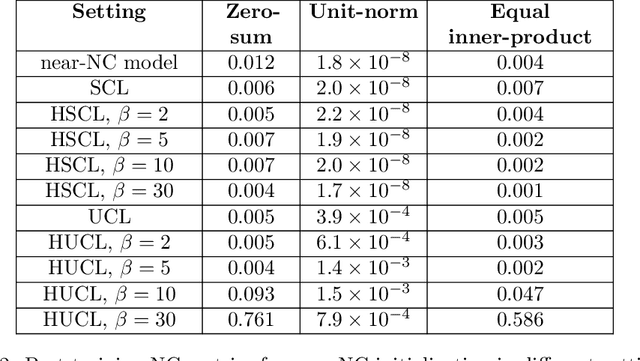
For a widely-studied data model and general loss and sample-hardening functions we prove that the Supervised Contrastive Learning (SCL), Hard-SCL (HSCL), and Unsupervised Contrastive Learning (UCL) risks are minimized by representations that exhibit Neural Collapse (NC), i.e., the class means form an Equianglular Tight Frame (ETF) and data from the same class are mapped to the same representation. We also prove that for any representation mapping, the HSCL and Hard-UCL (HUCL) risks are lower bounded by the corresponding SCL and UCL risks. Although the optimality of ETF is known for SCL, albeit only for InfoNCE loss, its optimality for HSCL and UCL under general loss and hardening functions is novel. Moreover, our proofs are much simpler, compact, and transparent. We empirically demonstrate, for the first time, that ADAM optimization of HSCL and HUCL risks with random initialization and suitable hardness levels can indeed converge to the NC geometry if we incorporate unit-ball or unit-sphere feature normalization. Without incorporating hard negatives or feature normalization, however, the representations learned via ADAM suffer from dimensional collapse (DC) and fail to attain the NC geometry.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge