Two-Dimensional Non-Line-of-Sight Scene Estimation from a Single Edge Occluder

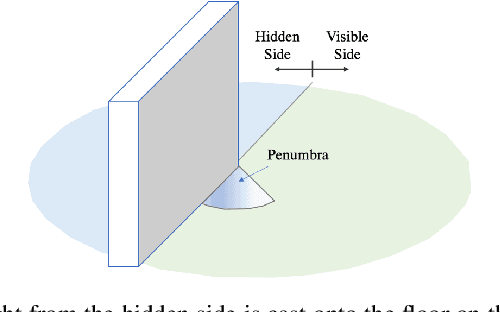
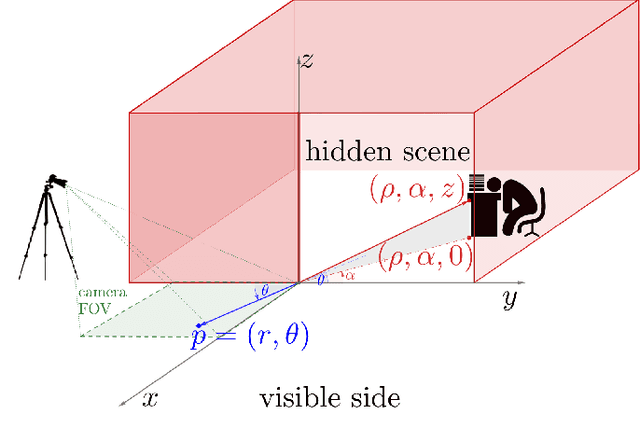
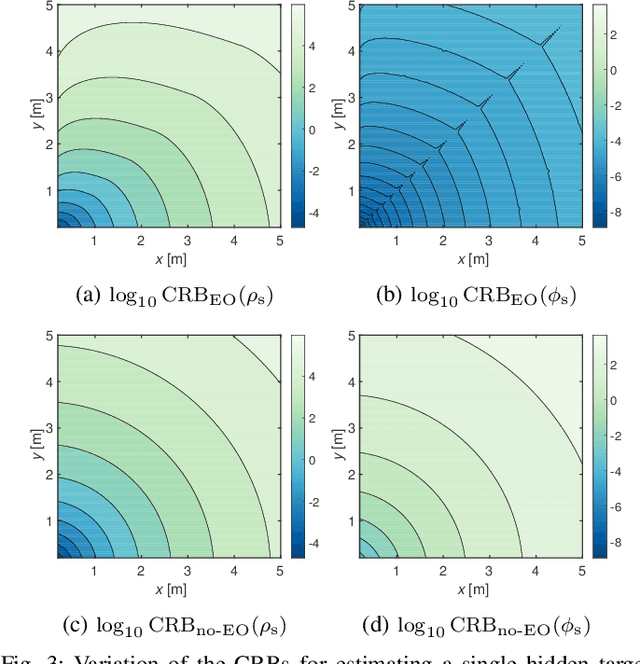
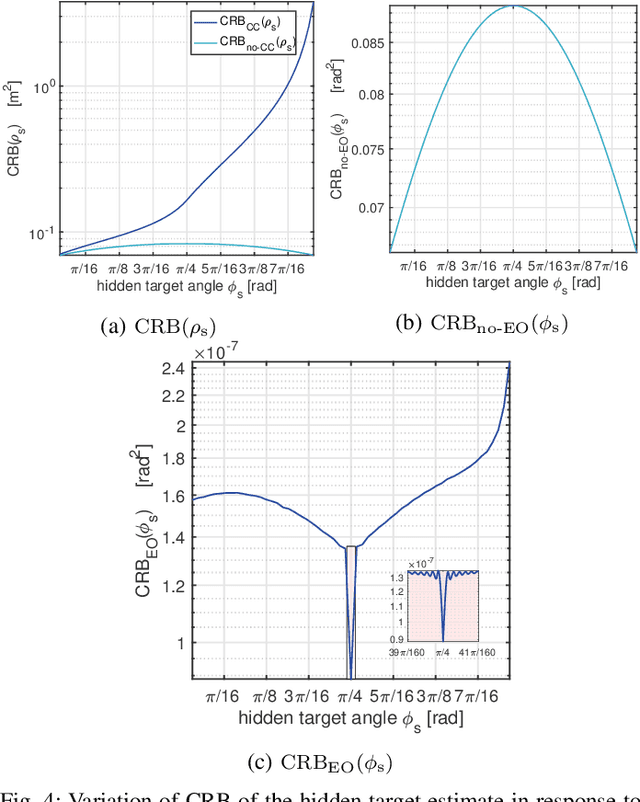
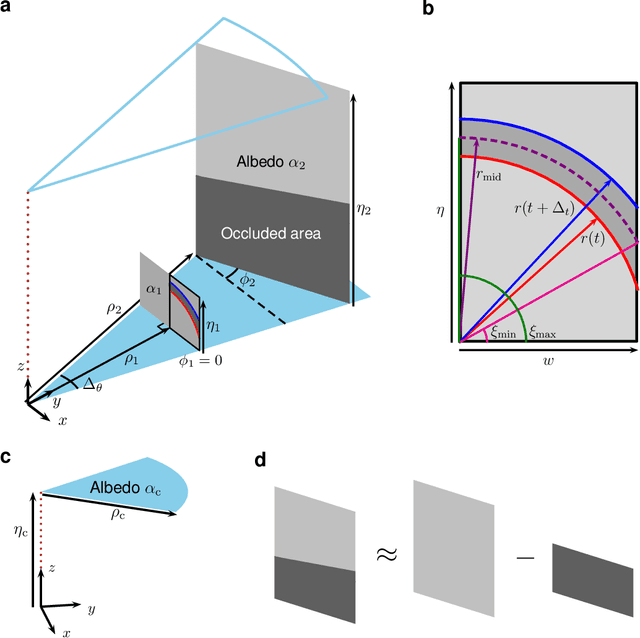
Passive non-line-of-sight imaging methods are often faster and stealthier than their active counterparts, requiring less complex and costly equipment. However, many of these methods exploit motion of an occluder or the hidden scene, or require knowledge or calibration of complicated occluders. The edge of a wall is a known and ubiquitous occluding structure that may be used as an aperture to image the region hidden behind it. Light from around the corner is cast onto the floor forming a fan-like penumbra rather than a sharp shadow. Subtle variations in the penumbra contain a remarkable amount of information about the hidden scene. Previous work has leveraged the vertical nature of the edge to demonstrate 1D (in angle measured around the corner) reconstructions of moving and stationary hidden scenery from as little as a single photograph of the penumbra. In this work, we introduce a second reconstruction dimension: range measured from the edge. We derive a new forward model, accounting for radial falloff, and propose two inversion algorithms to form 2D reconstructions from a single photograph of the penumbra. Performances of both algorithms are demonstrated on experimental data corresponding to several different hidden scene configurations. A Cramer-Rao bound analysis further demonstrates the feasibility (and utility) of the 2D corner camera.

Seeing Around Corners with Edge-Resolved Transient Imaging

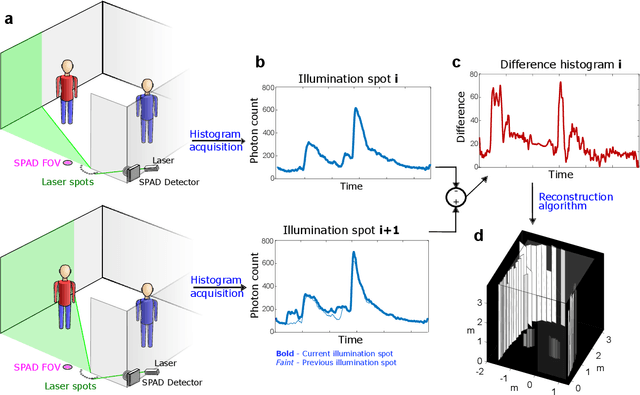
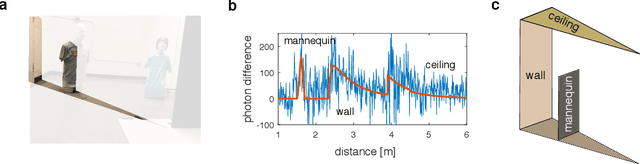
Non-line-of-sight (NLOS) imaging is a rapidly growing field seeking to form images of objects outside the field of view, with potential applications in search and rescue, reconnaissance, and even medical imaging. The critical challenge of NLOS imaging is that diffuse reflections scatter light in all directions, resulting in weak signals and a loss of directional information. To address this problem, we propose a method for seeing around corners that derives angular resolution from vertical edges and longitudinal resolution from the temporal response to a pulsed light source. We introduce an acquisition strategy, scene response model, and reconstruction algorithm that enable the formation of 2.5-dimensional representations -- a plan view plus heights -- and a 180$^{\circ}$ field of view (FOV) for large-scale scenes. Our experiments demonstrate accurate reconstructions of hidden rooms up to 3 meters in each dimension.

Beyond Binomial and Negative Binomial: Adaptation in Bernoulli Parameter Estimation

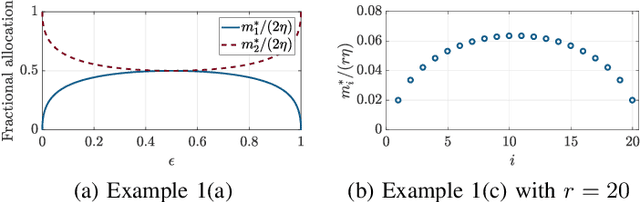
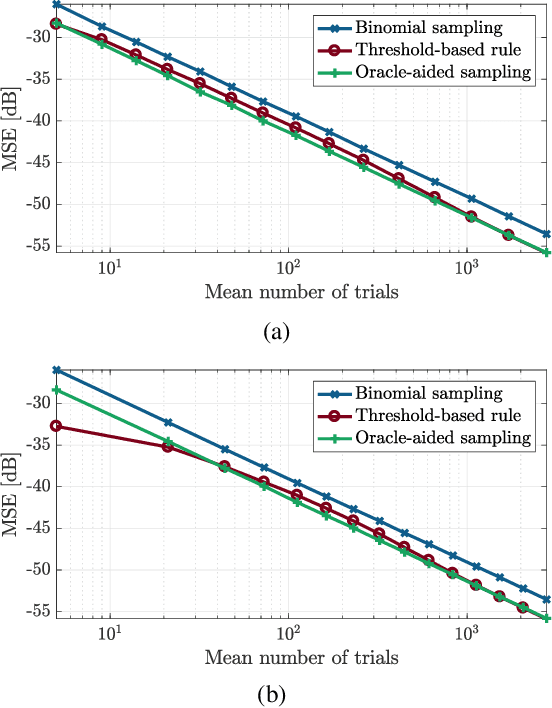
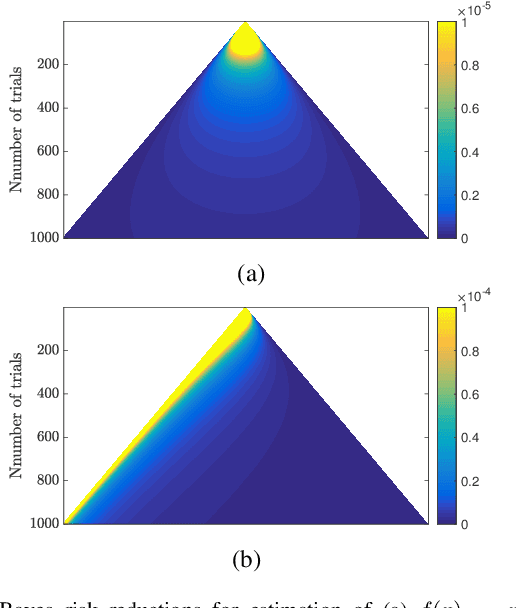
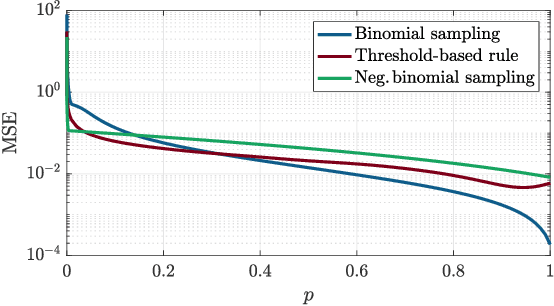
Estimating the parameter of a Bernoulli process arises in many applications, including photon-efficient active imaging where each illumination period is regarded as a single Bernoulli trial. Motivated by acquisition efficiency when multiple Bernoulli processes are of interest, we formulate the allocation of trials under a constraint on the mean as an optimal resource allocation problem. An oracle-aided trial allocation demonstrates that there can be a significant advantage from varying the allocation for different processes and inspires a simple trial allocation gain quantity. Motivated by realizing this gain without an oracle, we present a trellis-based framework for representing and optimizing stopping rules. Considering the convenient case of Beta priors, three implementable stopping rules with similar performances are explored, and the simplest of these is shown to asymptotically achieve the oracle-aided trial allocation. These approaches are further extended to estimating functions of a Bernoulli parameter. In simulations inspired by realistic active imaging scenarios, we demonstrate significant mean-squared error improvements: up to 4.36 dB for the estimation of p and up to 1.80 dB for the estimation of log p.