Absorption-Based, Passive Range Imaging from Hyperspectral Thermal Measurements

Passive hyperspectral long-wave infrared measurements are remarkably informative about the surroundings, such as remote object material composition, temperature, and range; and air temperature and gas concentrations. Remote object material and temperature determine the spectrum of thermal radiance, and range, air temperature, and gas concentrations determine how this spectrum is modified by propagation to the sensor. We computationally separate these phenomena, introducing a novel passive range imaging method based on atmospheric absorption of ambient thermal radiance. Previously demonstrated passive absorption-based ranging methods assume hot and highly emitting objects. However, the temperature variation in natural scenes is usually low, making range imaging challenging. Our method benefits from explicit consideration of air emission and parametric modeling of atmospheric absorption. To mitigate noise in low-contrast scenarios, we jointly estimate range and intrinsic object properties by exploiting a variety of absorption lines spread over the infrared spectrum. Along with Monte Carlo simulations that demonstrate the importance of regularization, temperature differentials, and availability of many spectral bands, we apply this method to long-wave infrared (8--13 $\mu$m) hyperspectral image data acquired from natural scenes with no active illumination. Range features from 15m to 150m are recovered, with good qualitative match to unaligned lidar data.

Non-Line-of-Sight Tracking and Mapping with an Active Corner Camera

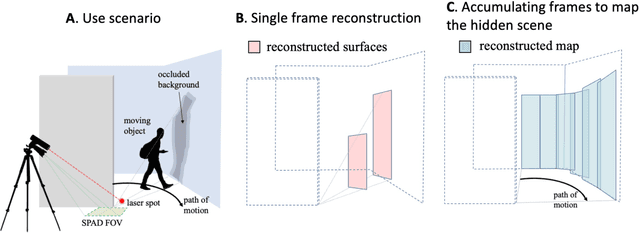
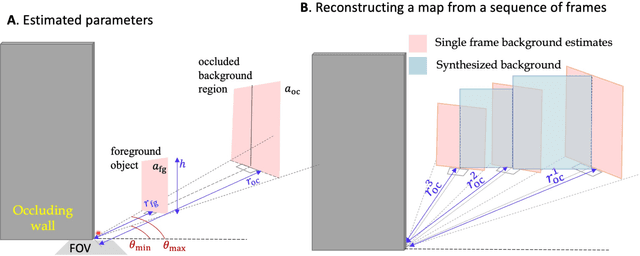
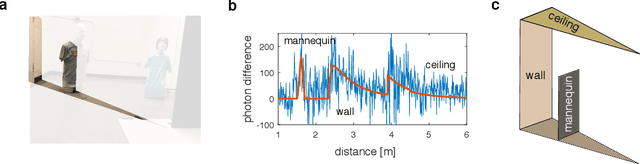
The ability to form non-line-of-sight (NLOS) images of changing scenes could be transformative in a variety of fields, including search and rescue, autonomous vehicle navigation, and reconnaissance. Most existing active NLOS methods illuminate the hidden scene using a pulsed laser directed at a relay surface and collect time-resolved measurements of returning light. The prevailing approaches include raster scanning of a rectangular grid on a vertical wall opposite the volume of interest to generate a collection of confocal measurements. These are inherently limited by the need for laser scanning. Methods that avoid laser scanning track the moving parts of the hidden scene as one or two point targets. In this work, based on more complete optical response modeling yet still without multiple illumination positions, we demonstrate accurate reconstructions of objects in motion and a 'map' of the stationary scenery behind them. The ability to count, localize, and characterize the sizes of hidden objects in motion, combined with mapping of the stationary hidden scene, could greatly improve indoor situational awareness in a variety of applications.

Online Beam Current Estimation in Particle Beam Microscopy

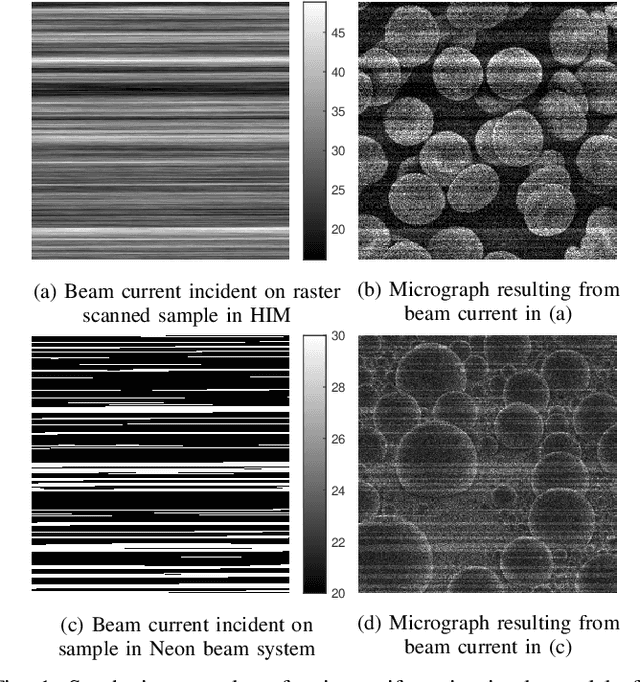
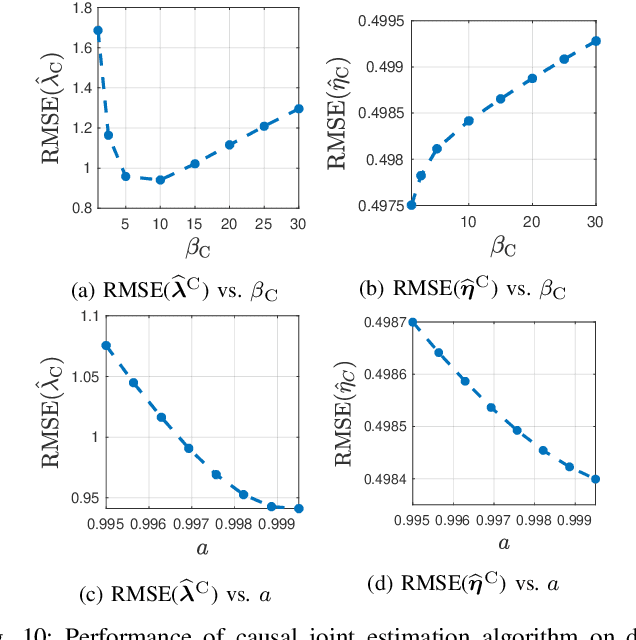
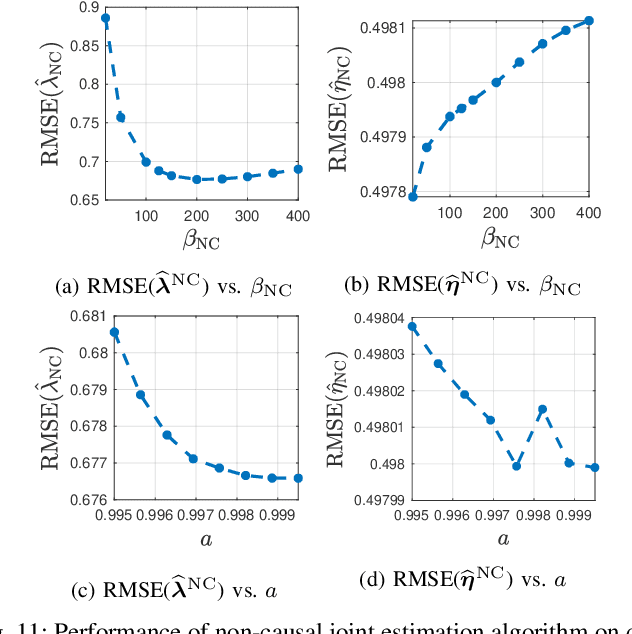
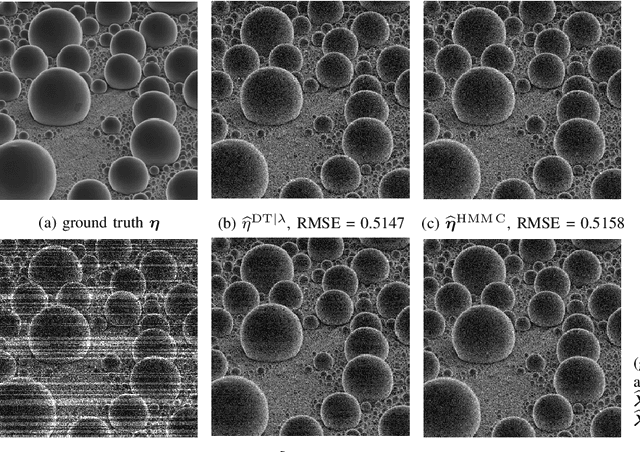
In conventional particle beam microscopy, knowledge of the beam current is essential for accurate micrograph formation and sample milling. This generally necessitates offline calibration of the instrument. In this work, we establish that beam current can be estimated online, from the same secondary electron count data that is used to form micrographs. Our methods depend on the recently introduced time-resolved measurement concept, which combines multiple short measurements at a single pixel and has previously been shown to partially mitigate the effect of beam current variation on micrograph accuracy. We analyze the problem of jointly estimating beam current and secondary electron yield using the Cramer-Rao bound. Joint estimators operating at a single pixel and estimators that exploit models for inter-pixel correlation and Markov beam current variation are proposed and tested on synthetic microscopy data. Our estimates of secondary electron yield that incorporate explicit beam current estimation beat state-of-the-art methods, resulting in micrograph accuracy nearly indistinguishable from what is obtained with perfect beam current knowledge. Our novel beam current estimation could help improve milling outcomes, prevent sample damage, and enable online instrument diagnostics.

Two-Dimensional Non-Line-of-Sight Scene Estimation from a Single Edge Occluder

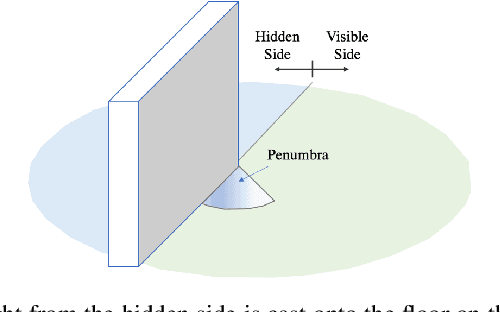
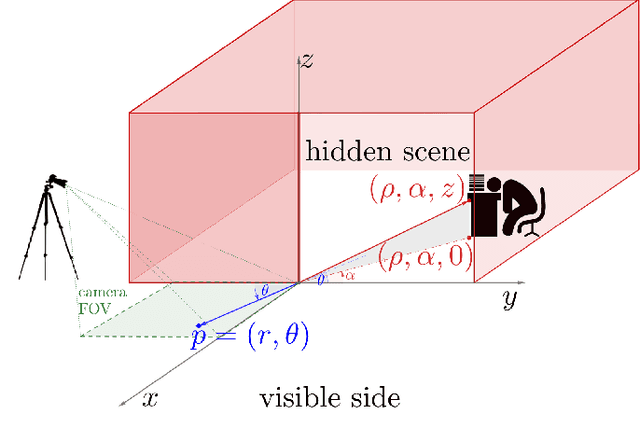
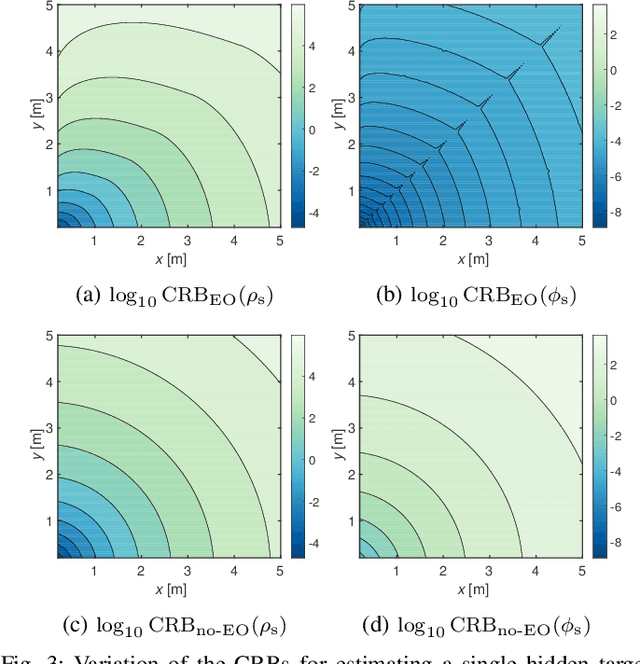
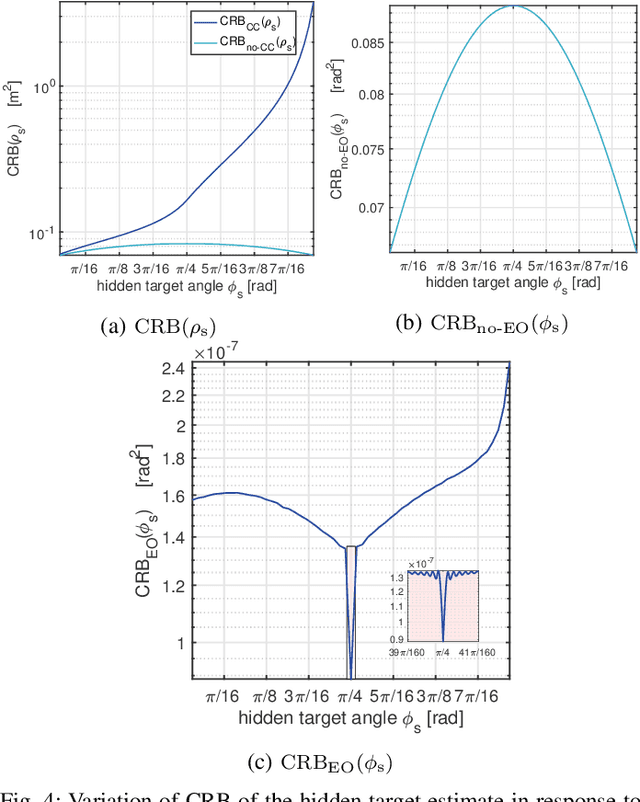
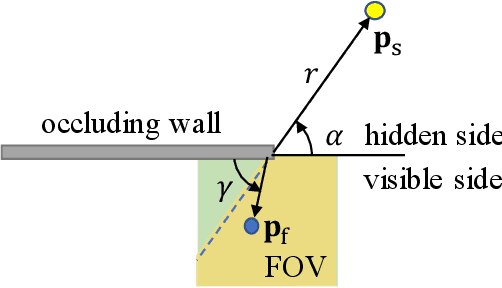
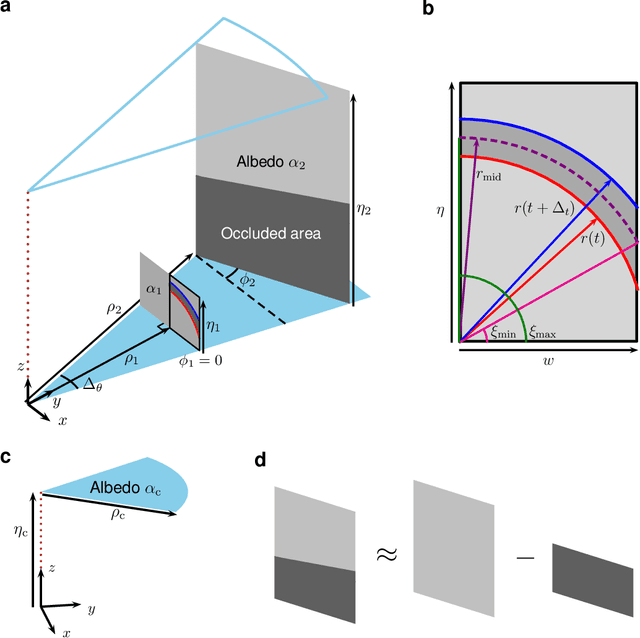
Passive non-line-of-sight imaging methods are often faster and stealthier than their active counterparts, requiring less complex and costly equipment. However, many of these methods exploit motion of an occluder or the hidden scene, or require knowledge or calibration of complicated occluders. The edge of a wall is a known and ubiquitous occluding structure that may be used as an aperture to image the region hidden behind it. Light from around the corner is cast onto the floor forming a fan-like penumbra rather than a sharp shadow. Subtle variations in the penumbra contain a remarkable amount of information about the hidden scene. Previous work has leveraged the vertical nature of the edge to demonstrate 1D (in angle measured around the corner) reconstructions of moving and stationary hidden scenery from as little as a single photograph of the penumbra. In this work, we introduce a second reconstruction dimension: range measured from the edge. We derive a new forward model, accounting for radial falloff, and propose two inversion algorithms to form 2D reconstructions from a single photograph of the penumbra. Performances of both algorithms are demonstrated on experimental data corresponding to several different hidden scene configurations. A Cramer-Rao bound analysis further demonstrates the feasibility (and utility) of the 2D corner camera.

Seeing Around Corners with Edge-Resolved Transient Imaging

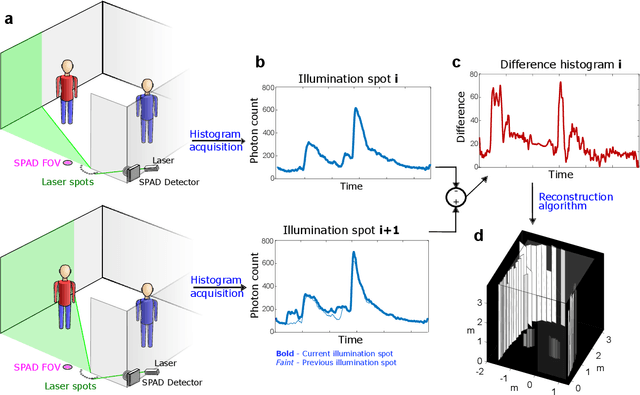
Non-line-of-sight (NLOS) imaging is a rapidly growing field seeking to form images of objects outside the field of view, with potential applications in search and rescue, reconnaissance, and even medical imaging. The critical challenge of NLOS imaging is that diffuse reflections scatter light in all directions, resulting in weak signals and a loss of directional information. To address this problem, we propose a method for seeing around corners that derives angular resolution from vertical edges and longitudinal resolution from the temporal response to a pulsed light source. We introduce an acquisition strategy, scene response model, and reconstruction algorithm that enable the formation of 2.5-dimensional representations -- a plan view plus heights -- and a 180$^{\circ}$ field of view (FOV) for large-scale scenes. Our experiments demonstrate accurate reconstructions of hidden rooms up to 3 meters in each dimension.

Beliefs and Expertise in Sequential Decision Making

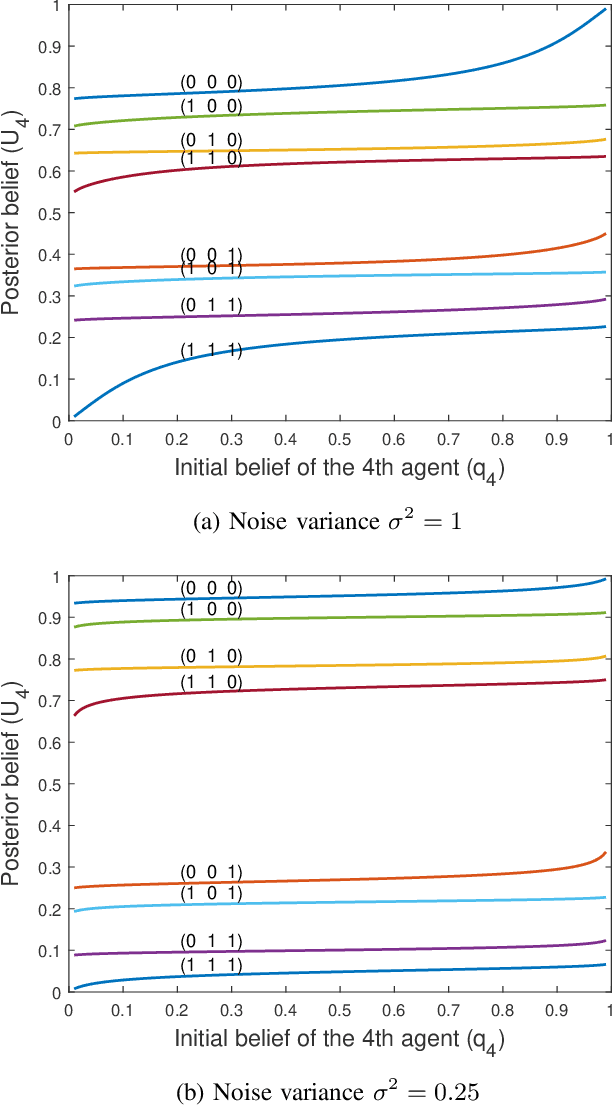
This work explores a sequential decision making problem with agents having diverse expertise and mismatched beliefs. We consider an $N$-agent sequential binary hypothesis test in which each agent sequentially makes a decision based not only on a private observation, but also on previous agents' decisions. In addition, the agents have their own beliefs instead of the true prior, and have varying expertise in terms of the noise variance in the private signal. We focus on the risk of the last-acting agent, where precedent agents are selfish. Thus, we call this advisor(s)-advisee sequential decision making. We first derive the optimal decision rule by recursive belief update and conclude, counterintuitively, that beliefs deviating from the true prior could be optimal in this setting. The impact of diverse noise levels (which means diverse expertise levels) in the two-agent case is also considered and the analytical properties of the optimal belief curves are given. These curves, for certain cases, resemble probability weighting functions from cumulative prospect theory, and so we also discuss the choice of Prelec weighting functions as an approximation for the optimal beliefs, and the possible psychophysical optimality of human beliefs. Next, we consider an advisor selection problem wherein the advisee of a certain belief chooses an advisor from a set of candidates with varying beliefs. We characterize the decision region for choosing such an advisor and argue that an advisee with beliefs varying from the true prior often ends up selecting a suboptimal advisor, indicating the need for a social planner. We close with a discussion on the implications of the study toward designing artificial intelligence systems for augmenting human intelligence.

Beyond Binomial and Negative Binomial: Adaptation in Bernoulli Parameter Estimation

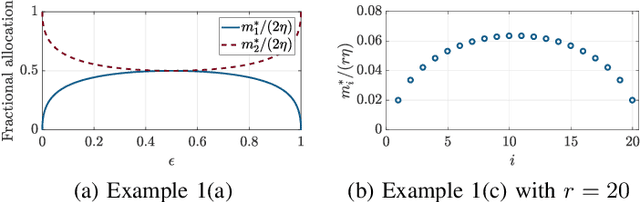
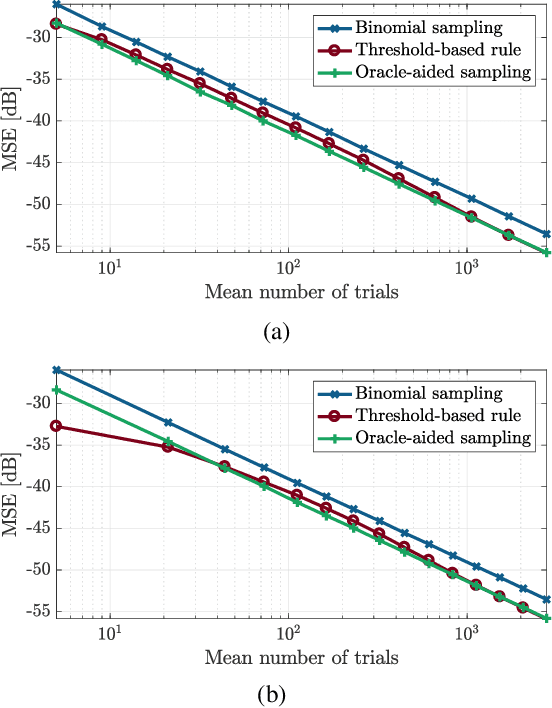
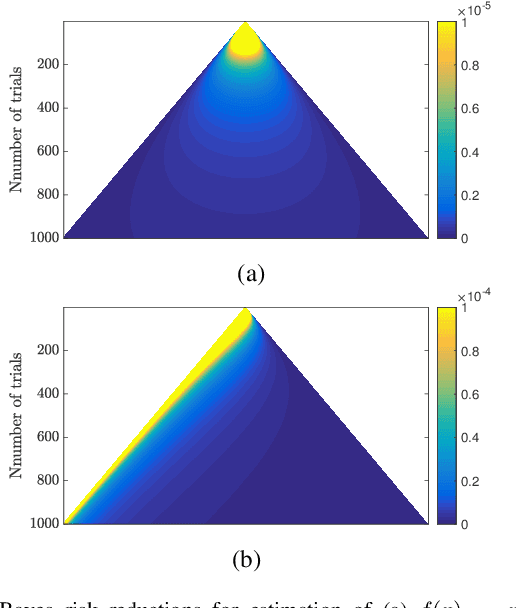
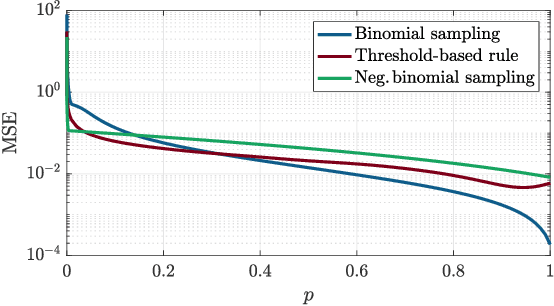
Estimating the parameter of a Bernoulli process arises in many applications, including photon-efficient active imaging where each illumination period is regarded as a single Bernoulli trial. Motivated by acquisition efficiency when multiple Bernoulli processes are of interest, we formulate the allocation of trials under a constraint on the mean as an optimal resource allocation problem. An oracle-aided trial allocation demonstrates that there can be a significant advantage from varying the allocation for different processes and inspires a simple trial allocation gain quantity. Motivated by realizing this gain without an oracle, we present a trellis-based framework for representing and optimizing stopping rules. Considering the convenient case of Beta priors, three implementable stopping rules with similar performances are explored, and the simplest of these is shown to asymptotically achieve the oracle-aided trial allocation. These approaches are further extended to estimating functions of a Bernoulli parameter. In simulations inspired by realistic active imaging scenarios, we demonstrate significant mean-squared error improvements: up to 4.36 dB for the estimation of p and up to 1.80 dB for the estimation of log p.