Beliefs and Expertise in Sequential Decision Making

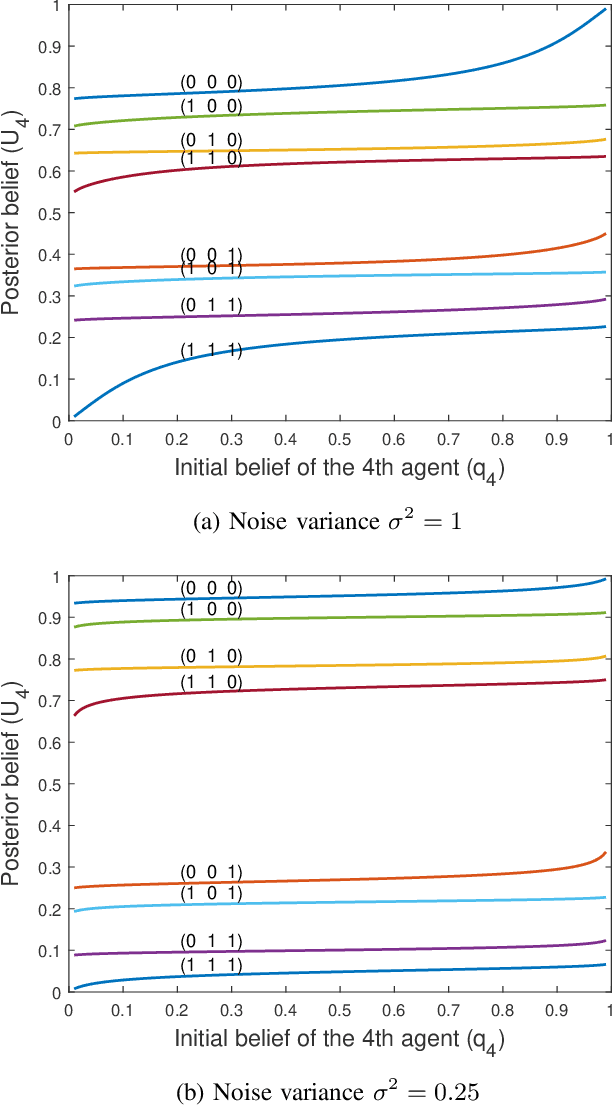
This work explores a sequential decision making problem with agents having diverse expertise and mismatched beliefs. We consider an $N$-agent sequential binary hypothesis test in which each agent sequentially makes a decision based not only on a private observation, but also on previous agents' decisions. In addition, the agents have their own beliefs instead of the true prior, and have varying expertise in terms of the noise variance in the private signal. We focus on the risk of the last-acting agent, where precedent agents are selfish. Thus, we call this advisor(s)-advisee sequential decision making. We first derive the optimal decision rule by recursive belief update and conclude, counterintuitively, that beliefs deviating from the true prior could be optimal in this setting. The impact of diverse noise levels (which means diverse expertise levels) in the two-agent case is also considered and the analytical properties of the optimal belief curves are given. These curves, for certain cases, resemble probability weighting functions from cumulative prospect theory, and so we also discuss the choice of Prelec weighting functions as an approximation for the optimal beliefs, and the possible psychophysical optimality of human beliefs. Next, we consider an advisor selection problem wherein the advisee of a certain belief chooses an advisor from a set of candidates with varying beliefs. We characterize the decision region for choosing such an advisor and argue that an advisee with beliefs varying from the true prior often ends up selecting a suboptimal advisor, indicating the need for a social planner. We close with a discussion on the implications of the study toward designing artificial intelligence systems for augmenting human intelligence.

Trusted Multi-Party Computation and Verifiable Simulations: A Scalable Blockchain Approach

Large-scale computational experiments, often running over weeks and over large datasets, are used extensively in fields such as epidemiology, meteorology, computational biology, and healthcare to understand phenomena, and design high-stakes policies affecting everyday health and economy. For instance, the OpenMalaria framework is a computationally-intensive simulation used by various non-governmental and governmental agencies to understand malarial disease spread and effectiveness of intervention strategies, and subsequently design healthcare policies. Given that such shared results form the basis of inferences drawn, technological solutions designed, and day-to-day policies drafted, it is essential that the computations are validated and trusted. In particular, in a multi-agent environment involving several independent computing agents, a notion of trust in results generated by peers is critical in facilitating transparency, accountability, and collaboration. Using a novel combination of distributed validation of atomic computation blocks and a blockchain-based immutable audits mechanism, this work proposes a universal framework for distributed trust in computations. In particular we address the scalaibility problem by reducing the storage and communication costs using a lossy compression scheme. This framework guarantees not only verifiability of final results, but also the validity of local computations, and its cost-benefit tradeoffs are studied using a synthetic example of training a neural network.

Universal Joint Image Clustering and Registration using Partition Information

We consider the problem of universal joint clustering and registration of images and define algorithms using multivariate information functionals. We first study registering two images using maximum mutual information and prove its asymptotic optimality. We then show the shortcomings of pairwise registration in multi-image registration, and design an asymptotically optimal algorithm based on multiinformation. Further, we define a novel multivariate information functional to perform joint clustering and registration of images, and prove consistency of the algorithm. Finally, we consider registration and clustering of numerous limited-resolution images, defining algorithms that are order-optimal in scaling of number of pixels in each image with the number of images.

Universal Clustering via Crowdsourcing

Consider unsupervised clustering of objects drawn from a discrete set, through the use of human intelligence available in crowdsourcing platforms. This paper defines and studies the problem of universal clustering using responses of crowd workers, without knowledge of worker reliability or task difficulty. We model stochastic worker response distributions by incorporating traits of memory for similar objects and traits of distance among differing objects. We are particularly interested in two limiting worker types---temporary workers who retain no memory of responses and long-term workers with memory. We first define clustering algorithms for these limiting cases and then integrate them into an algorithm for the unified worker model. We prove asymptotic consistency of the algorithms and establish sufficient conditions on the sample complexity of the algorithm. Converse arguments establish necessary conditions on sample complexity, proving that the defined algorithms are asymptotically order-optimal in cost.