Deep Minimax Classifiers for Imbalanced Datasets with a Small Number of Minority Samples

The concept of a minimax classifier is well-established in statistical decision theory, but its implementation via neural networks remains challenging, particularly in scenarios with imbalanced training data having a limited number of samples for minority classes. To address this issue, we propose a novel minimax learning algorithm designed to minimize the risk of worst-performing classes. Our algorithm iterates through two steps: a minimization step that trains the model based on a selected target prior, and a maximization step that updates the target prior towards the adversarial prior for the trained model. In the minimization, we introduce a targeted logit-adjustment loss function that efficiently identifies optimal decision boundaries under the target prior. Moreover, based on a new prior-dependent generalization bound that we obtained, we theoretically prove that our loss function has a better generalization capability than existing loss functions. During the maximization, we refine the target prior by shifting it towards the adversarial prior, depending on the worst-performing classes rather than on per-class risk estimates. Our maximization method is particularly robust in the regime of a small number of samples. Additionally, to adapt to overparameterized neural networks, we partition the entire training dataset into two subsets: one for model training during the minimization step and the other for updating the target prior during the maximization step. Our proposed algorithm has a provable convergence property, and empirical results indicate that our algorithm performs better than or is comparable to existing methods. All codes are publicly available at https://github.com/hansung-choi/TLA-linear-ascent.

Integrated Communication and Binary State Detection Under Unequal Error Constraints

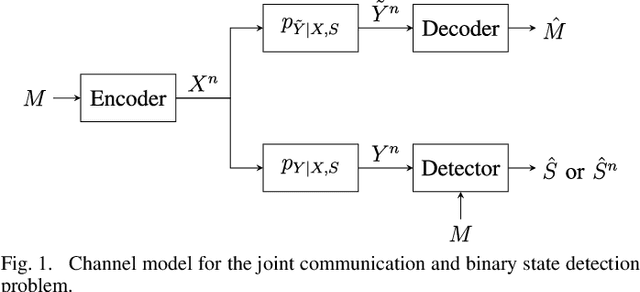
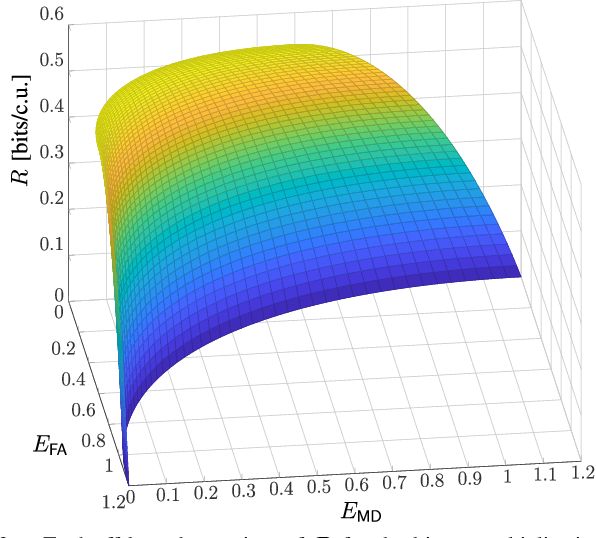
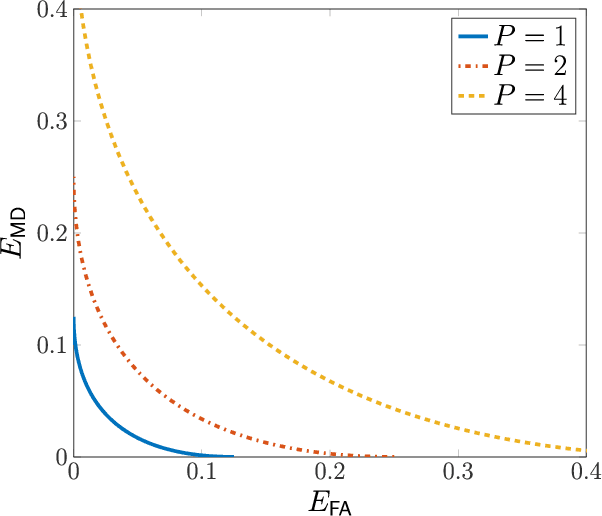
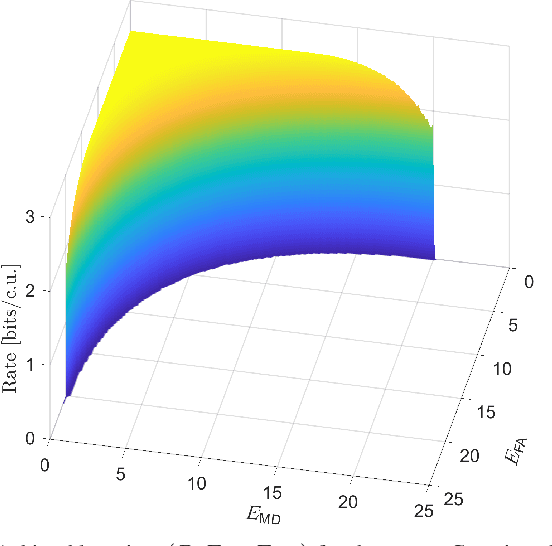
This work considers a problem of integrated sensing and communication (ISAC) in which the goal of sensing is to detect a binary state. Unlike most approaches that minimize the total detection error probability, in our work, we disaggregate the error probability into false alarm and missed detection probabilities and investigate their information-theoretic three-way tradeoff including communication data rate. We consider a broadcast channel that consists of a transmitter, a communication receiver, and a detector where the receiver's and the detector's channels are affected by an unknown binary state. We consider and present results on two different state-dependent models. In the first setting, the state is fixed throughout the entire transmission, for which we fully characterize the optimal three-way tradeoff between the coding rate for communication and the two possibly nonidentical error exponents for sensing in the asymptotic regime. The achievability and converse proofs rely on the analysis of the cumulant-generating function of the log-likelihood ratio. In the second setting, the state changes every symbol in an independently and identically distributed (i.i.d.) manner, for which we characterize the optimal tradeoff region based on the analysis of the receiver operating characteristic (ROC) curves.

On the Fundamental Tradeoff of Joint Communication and Quickest Change Detection

In this work, we take the initiative in studying the fundamental tradeoff between communication and quickest change detection (QCD) under an integrated sensing and communication setting. We formally establish a joint communication and sensing problem for quickest change detection. Then, by utilizing constant subblock-composition codes and a modified QuSum detection rule, which we call subblock QuSum (SQS), we provide an inner bound on the fundamental tradeoff between communication rate and change point detection delay in the asymptotic regime of vanishing false alarm rate. We further provide a partial converse that matches our inner bound for a certain class of codes. This implies that the SQS detection strategy is asymptotically optimal for our codes as the false alarm rate constraint vanishes. We also present some canonical examples of the tradeoff region for a binary channel, a scalar Gaussian channel, and a MIMO Gaussian channel.

Communication-Efficient and Drift-Robust Federated Learning via Elastic Net

Federated learning (FL) is a distributed method to train a global model over a set of local clients while keeping data localized. It reduces the risks of privacy and security but faces important challenges including expensive communication costs and client drift issues. To address these issues, we propose FedElasticNet, a communication-efficient and drift-robust FL framework leveraging the elastic net. It repurposes two types of the elastic net regularizers (i.e., $\ell_1$ and $\ell_2$ penalties on the local model updates): (1) the $\ell_1$-norm regularizer sparsifies the local updates to reduce the communication costs and (2) the $\ell_2$-norm regularizer resolves the client drift problem by limiting the impact of drifting local updates due to data heterogeneity. FedElasticNet is a general framework for FL; hence, without additional costs, it can be integrated into prior FL techniques, e.g., FedAvg, FedProx, SCAFFOLD, and FedDyn. We show that our framework effectively resolves the communication cost and client drift problems simultaneously.

Improved Input Reprogramming for GAN Conditioning

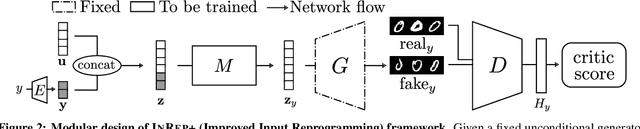
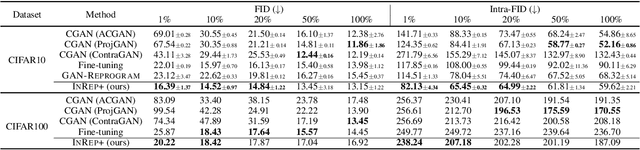
We study the GAN conditioning problem, whose goal is to convert a pretrained unconditional GAN into a conditional GAN using labeled data. We first identify and analyze three approaches to this problem -- conditional GAN training from scratch, fine-tuning, and input reprogramming. Our analysis reveals that when the amount of labeled data is small, input reprogramming performs the best. Motivated by real-world scenarios with scarce labeled data, we focus on the input reprogramming approach and carefully analyze the existing algorithm. After identifying a few critical issues of the previous input reprogramming approach, we propose a new algorithm called InRep+. Our algorithm InRep+ addresses the existing issues with the novel uses of invertible neural networks and Positive-Unlabeled (PU) learning. Via extensive experiments, we show that InRep+ outperforms all existing methods, particularly when label information is scarce, noisy, and/or imbalanced. For instance, for the task of conditioning a CIFAR10 GAN with 1% labeled data, InRep+ achieves an average Intra-FID of 76.24, whereas the second-best method achieves 114.51.

Beliefs and Expertise in Sequential Decision Making

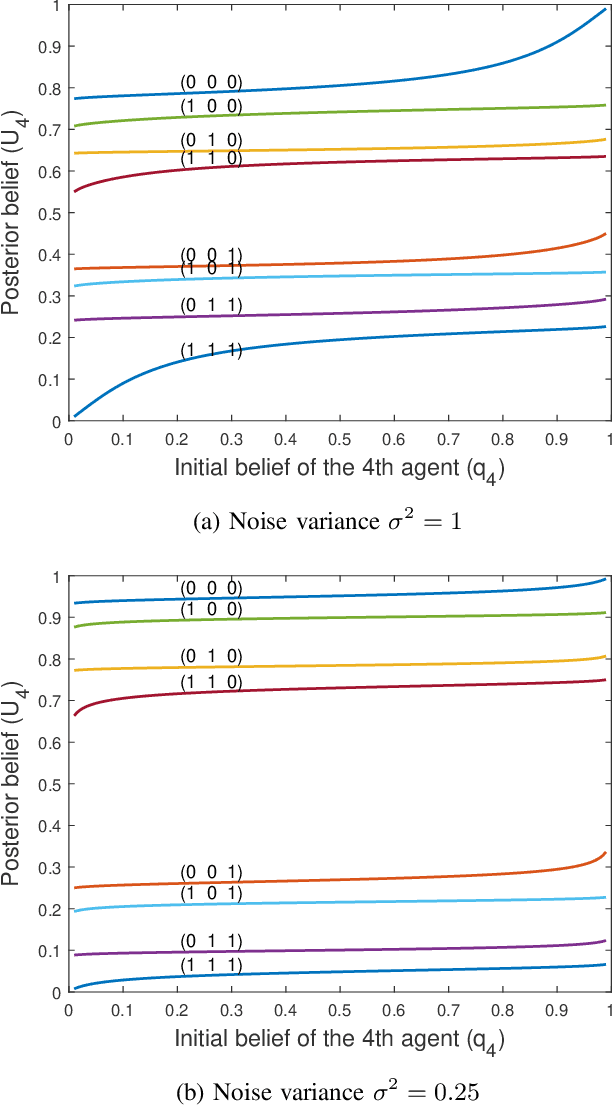
This work explores a sequential decision making problem with agents having diverse expertise and mismatched beliefs. We consider an $N$-agent sequential binary hypothesis test in which each agent sequentially makes a decision based not only on a private observation, but also on previous agents' decisions. In addition, the agents have their own beliefs instead of the true prior, and have varying expertise in terms of the noise variance in the private signal. We focus on the risk of the last-acting agent, where precedent agents are selfish. Thus, we call this advisor(s)-advisee sequential decision making. We first derive the optimal decision rule by recursive belief update and conclude, counterintuitively, that beliefs deviating from the true prior could be optimal in this setting. The impact of diverse noise levels (which means diverse expertise levels) in the two-agent case is also considered and the analytical properties of the optimal belief curves are given. These curves, for certain cases, resemble probability weighting functions from cumulative prospect theory, and so we also discuss the choice of Prelec weighting functions as an approximation for the optimal beliefs, and the possible psychophysical optimality of human beliefs. Next, we consider an advisor selection problem wherein the advisee of a certain belief chooses an advisor from a set of candidates with varying beliefs. We characterize the decision region for choosing such an advisor and argue that an advisee with beliefs varying from the true prior often ends up selecting a suboptimal advisor, indicating the need for a social planner. We close with a discussion on the implications of the study toward designing artificial intelligence systems for augmenting human intelligence.