GSR: A Generalized Symbolic Regression Approach
Paper and Code
May 31, 2022
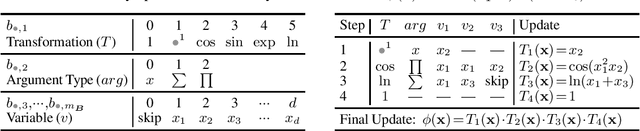

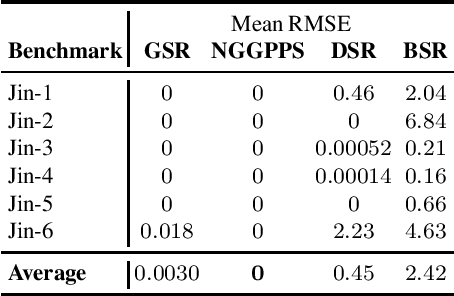
Identifying the mathematical relationships that best describe a dataset remains a very challenging problem in machine learning, and is known as Symbolic Regression (SR). In contrast to neural networks which are often treated as black boxes, SR attempts to gain insight into the underlying relationships between the independent variables and the target variable of a given dataset by assembling analytical functions. In this paper, we present GSR, a Generalized Symbolic Regression approach, by modifying the conventional SR optimization problem formulation, while keeping the main SR objective intact. In GSR, we infer mathematical relationships between the independent variables and some transformation of the target variable. We constrain our search space to a weighted sum of basis functions, and propose a genetic programming approach with a matrix-based encoding scheme. We show that our GSR method outperforms several state-of-the-art methods on the well-known SR benchmark problem sets. Finally, we highlight the strengths of GSR by introducing SymSet, a new SR benchmark set which is more challenging relative to the existing benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge