RL in Latent MDPs is Tractable: Online Guarantees via Off-Policy Evaluation

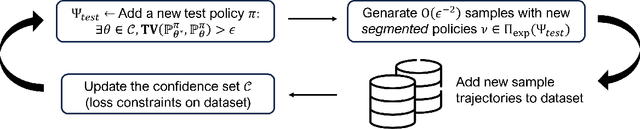
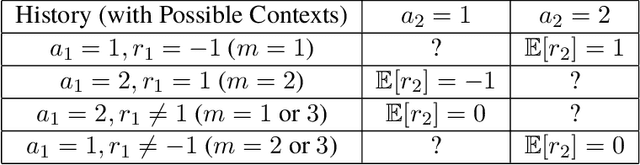
In many real-world decision problems there is partially observed, hidden or latent information that remains fixed throughout an interaction. Such decision problems can be modeled as Latent Markov Decision Processes (LMDPs), where a latent variable is selected at the beginning of an interaction and is not disclosed to the agent. In the last decade, there has been significant progress in solving LMDPs under different structural assumptions. However, for general LMDPs, there is no known learning algorithm that provably matches the existing lower bound~\cite{kwon2021rl}. We introduce the first sample-efficient algorithm for LMDPs without any additional structural assumptions. Our result builds off a new perspective on the role of off-policy evaluation guarantees and coverage coefficients in LMDPs, a perspective, that has been overlooked in the context of exploration in partially observed environments. Specifically, we establish a novel off-policy evaluation lemma and introduce a new coverage coefficient for LMDPs. Then, we show how these can be used to derive near-optimal guarantees of an optimistic exploration algorithm. These results, we believe, can be valuable for a wide range of interactive learning problems beyond LMDPs, and especially, for partially observed environments.