Shuchi Chawla
Approximating Pandora's Box with Correlations
Aug 30, 2021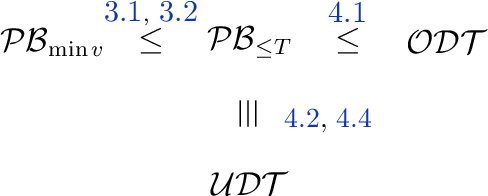
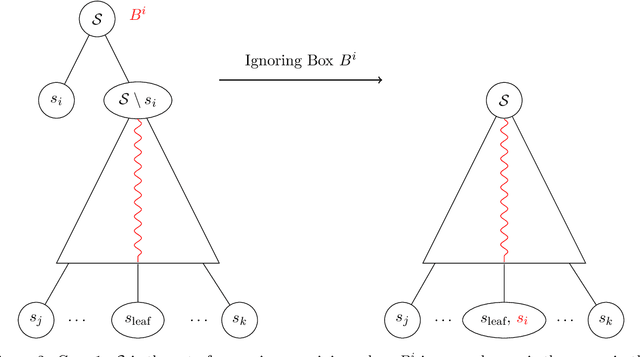
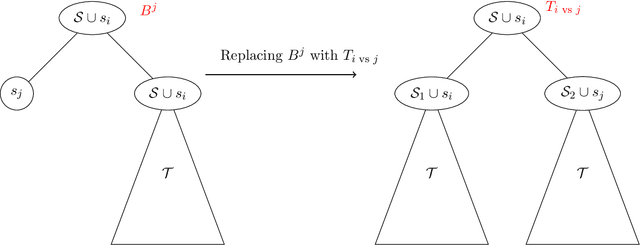
Abstract:The Pandora's Box problem asks to find a search strategy over $n$ alternatives given stochastic information about their values, aiming to minimize the sum of the search cost and the value of the chosen alternative. Even though the case of independently distributed values is well understood, our algorithmic understanding of the problem is very limited once the independence assumption is dropped. Our work aims to characterize the complexity of approximating the Pandora's Box problem under correlated value distributions. To that end, we present a general reduction to a simpler version of Pandora's Box, that only asks to find a value below a certain threshold, and eliminates the need to reason about future values that will arise during the search. Using this general tool, we study two cases of correlation; the case of explicitly given distributions of support $m$ and the case of mixtures of $m$ product distributions. $\bullet$ In the first case, we connect Pandora's Box to the well studied problem of Optimal Decision Tree, obtaining an $O(\log m)$ approximation but also showing that the problem is strictly easier as it is equivalent (up to constant factors) to the Uniform Decision Tree problem. $\bullet$ In the case of mixtures of product distributions, the problem is again related to the noisy variant of Optimal Decision Tree which is significantly more challenging. We give a constant-factor approximation that runs in time $n^{ \tilde O( m^2/\varepsilon^2 ) }$ for $m$ mixture components whose marginals on every alternative are either identical or separated in TV distance by $\varepsilon$.
Fairness in ad auctions through inverse proportionality
Mar 31, 2020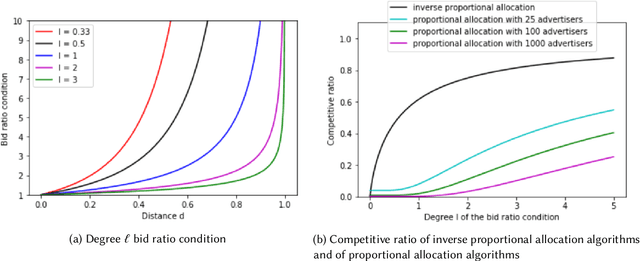

Abstract:We study the tradeoff between social welfare maximization and fairness in the context of ad auctions. We study an ad auction setting where users arrive in an online fashion, $k$ advertisers submit bids for each user, and the auction assigns a distribution over ads to the user. Following the works of Dwork and Ilvento (2019) and Chawla et al. (2020), our goal is to design a truthful auction that satisfies multiple-task fairness in its outcomes: informally speaking, users that are similar to each other should obtain similar allocations of ads. We develop a new class of allocation algorithms that we call inverse-proportional allocation. These allocation algorithms are truthful, online, and do not explicitly need to know the fairness constraint over the users. In terms of fairness, they guarantee fair outcomes as long as every advertiser's bids are non-discriminatory across users. In terms of social welfare, inverse-proportional allocation achieves a constant factor approximation in social welfare against the optimal (unfair) allocation, independent of the number of advertisers in the system. In this respect, these allocation algorithms greatly surpass the guarantees achieved in previous work; in fact, they achieve the optimal tradeoffs between fairness and social welfare in some contexts. We also extend our results to broader notions of fairness that we call subset fairness.
Individual Fairness in Sponsored Search Auctions
Jun 20, 2019

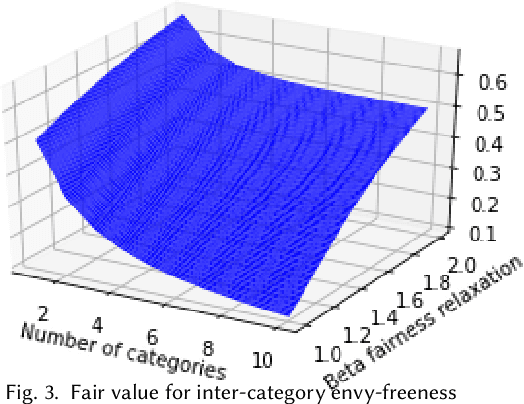
Abstract:Fairness in advertising is a topic of particular interest in both the computer science and economics literatures, supported by theoretical and empirical observations. We initiate the study of tradeoffs between individual fairness and performance in online advertising, where advertisers place bids on ad slots for each user and the platform must determine which ads to display. Our main focus is to investigate the "cost of fairness": more specifically, whether a fair allocation mechanism can achieve utility close to that of a utility-optimal unfair mechanism. Motivated by practice, we consider both the case of many advertisers in a single category, e.g. sponsored results on a job search website, and ads spanning multiple categories, e.g. personalized display advertising on a social networking site, and show the tradeoffs are inherently different in these settings. We prove lower and upper bounds on the cost of fairness for each of these settings. For the single category setting, we show constraints on the "fairness" of advertisers' bids are necessary to achieve good utility. Moreover, with bid fairness constraints, we construct a mechanism that simultaneously achieves a high utility and a strengthening of typical fairness constraints that we call total variation fairness. For the multiple category setting, we show that fairness relaxations are necessary to achieve good utility. We consider a relaxed definition based on user-specified category preferences that we call user-directed fairness, and we show that with this fairness notion a high utility is achievable. Finally, we show that our mechanisms in the single and multiple category settings compose well, yielding a high utility combined mechanism that satisfies user-directed fairness across categories and conditional total variation fairness within categories.
Truth and Regret in Online Scheduling
Mar 01, 2017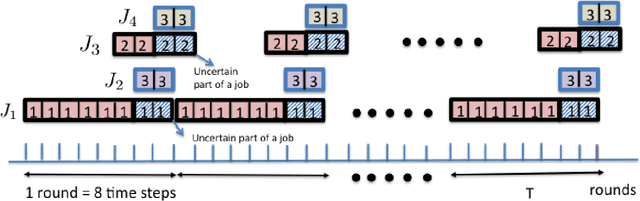


Abstract:We consider a scheduling problem where a cloud service provider has multiple units of a resource available over time. Selfish clients submit jobs, each with an arrival time, deadline, length, and value. The service provider's goal is to implement a truthful online mechanism for scheduling jobs so as to maximize the social welfare of the schedule. Recent work shows that under a stochastic assumption on job arrivals, there is a single-parameter family of mechanisms that achieves near-optimal social welfare. We show that given any such family of near-optimal online mechanisms, there exists an online mechanism that in the worst case performs nearly as well as the best of the given mechanisms. Our mechanism is truthful whenever the mechanisms in the given family are truthful and prompt, and achieves optimal (within constant factors) regret. We model the problem of competing against a family of online scheduling mechanisms as one of learning from expert advice. A primary challenge is that any scheduling decisions we make affect not only the payoff at the current step, but also the resource availability and payoffs in future steps. Furthermore, switching from one algorithm (a.k.a. expert) to another in an online fashion is challenging both because it requires synchronization with the state of the latter algorithm as well as because it affects the incentive structure of the algorithms. We further show how to adapt our algorithm to a non-clairvoyant setting where job lengths are unknown until jobs are run to completion. Once again, in this setting, we obtain truthfulness along with asymptotically optimal regret (within poly-logarithmic factors).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge