Approximating Pandora's Box with Correlations
Paper and Code
Aug 30, 2021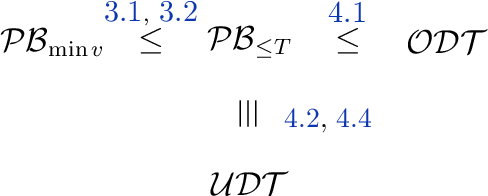
The Pandora's Box problem asks to find a search strategy over $n$ alternatives given stochastic information about their values, aiming to minimize the sum of the search cost and the value of the chosen alternative. Even though the case of independently distributed values is well understood, our algorithmic understanding of the problem is very limited once the independence assumption is dropped. Our work aims to characterize the complexity of approximating the Pandora's Box problem under correlated value distributions. To that end, we present a general reduction to a simpler version of Pandora's Box, that only asks to find a value below a certain threshold, and eliminates the need to reason about future values that will arise during the search. Using this general tool, we study two cases of correlation; the case of explicitly given distributions of support $m$ and the case of mixtures of $m$ product distributions. $\bullet$ In the first case, we connect Pandora's Box to the well studied problem of Optimal Decision Tree, obtaining an $O(\log m)$ approximation but also showing that the problem is strictly easier as it is equivalent (up to constant factors) to the Uniform Decision Tree problem. $\bullet$ In the case of mixtures of product distributions, the problem is again related to the noisy variant of Optimal Decision Tree which is significantly more challenging. We give a constant-factor approximation that runs in time $n^{ \tilde O( m^2/\varepsilon^2 ) }$ for $m$ mixture components whose marginals on every alternative are either identical or separated in TV distance by $\varepsilon$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge