Adaptive and Optimal Second-order Optimistic Methods for Minimax Optimization

We propose adaptive, line search-free second-order methods with optimal rate of convergence for solving convex-concave min-max problems. By means of an adaptive step size, our algorithms feature a simple update rule that requires solving only one linear system per iteration, eliminating the need for line search or backtracking mechanisms. Specifically, we base our algorithms on the optimistic method and appropriately combine it with second-order information. Moreover, distinct from common adaptive schemes, we define the step size recursively as a function of the gradient norm and the prediction error in the optimistic update. We first analyze a variant where the step size requires knowledge of the Lipschitz constant of the Hessian. Under the additional assumption of Lipschitz continuous gradients, we further design a parameter-free version by tracking the Hessian Lipschitz constant locally and ensuring the iterates remain bounded. We also evaluate the practical performance of our algorithm by comparing it to existing second-order algorithms for minimax optimization.

Online Learning Guided Curvature Approximation: A Quasi-Newton Method with Global Non-Asymptotic Superlinear Convergence

Quasi-Newton algorithms are among the most popular iterative methods for solving unconstrained minimization problems, largely due to their favorable superlinear convergence property. However, existing results for these algorithms are limited as they provide either (i) a global convergence guarantee with an asymptotic superlinear convergence rate, or (ii) a local non-asymptotic superlinear rate for the case that the initial point and the initial Hessian approximation are chosen properly. Furthermore, these results are not composable, since when the iterates of the globally convergent methods reach the region of local superlinear convergence, it cannot be guaranteed the Hessian approximation matrix will satisfy the required conditions for a non-asymptotic local superlienar convergence rate. In this paper, we close this gap and present the first globally convergent quasi-Newton method with an explicit non-asymptotic superlinear convergence rate. Unlike classical quasi-Newton methods, we build our algorithm upon the hybrid proximal extragradient method and propose a novel online learning framework for updating the Hessian approximation matrices. Specifically, guided by the convergence analysis, we formulate the Hessian approximation update as an online convex optimization problem in the space of matrices, and relate the bounded regret of the online problem to the superlinear convergence of our method.

Exploiting Local Convergence of Quasi-Newton Methods Globally: Adaptive Sample Size Approach

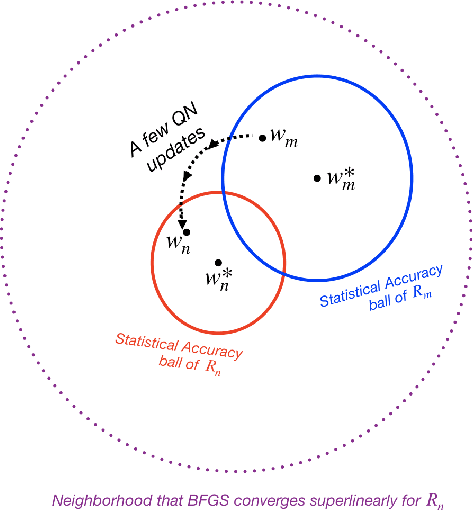
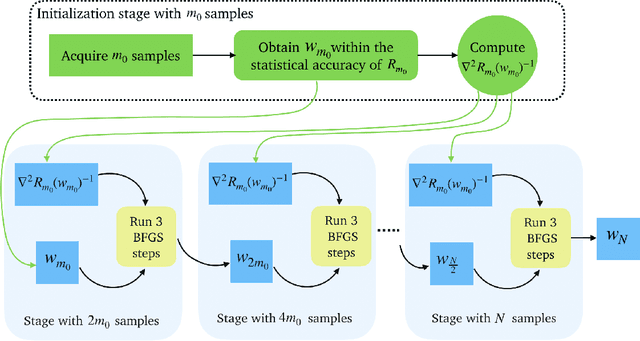
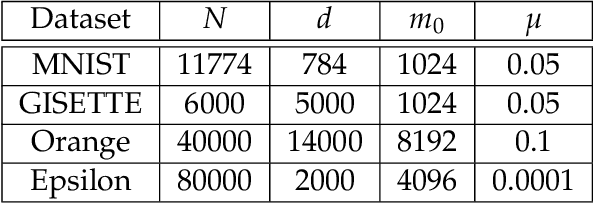
In this paper, we study the application of quasi-Newton methods for solving empirical risk minimization (ERM) problems defined over a large dataset. Traditional deterministic and stochastic quasi-Newton methods can be executed to solve such problems; however, it is known that their global convergence rate may not be better than first-order methods, and their local superlinear convergence only appears towards the end of the learning process. In this paper, we use an adaptive sample size scheme that exploits the superlinear convergence of quasi-Newton methods globally and throughout the entire learning process. The main idea of the proposed adaptive sample size algorithms is to start with a small subset of data points and solve their corresponding ERM problem within its statistical accuracy, and then enlarge the sample size geometrically and use the optimal solution of the problem corresponding to the smaller set as an initial point for solving the subsequent ERM problem with more samples. We show that if the initial sample size is sufficiently large and we use quasi-Newton methods to solve each subproblem, the subproblems can be solved superlinearly fast (after at most three iterations), as we guarantee that the iterates always stay within a neighborhood that quasi-Newton methods converge superlinearly. Numerical experiments on various datasets confirm our theoretical results and demonstrate the computational advantages of our method.

Non-asymptotic Superlinear Convergence of Standard Quasi-Newton Methods

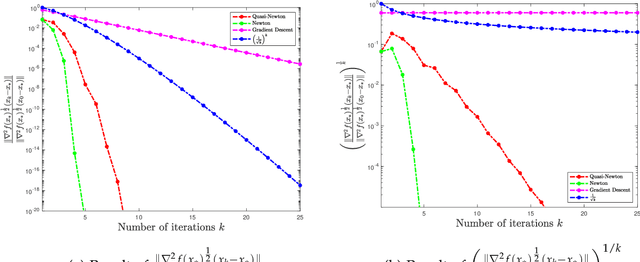
In this paper, we study the non-asymptotic superlinear convergence rate of DFP and BFGS, which are two well-known quasi-Newton methods. The asymptotic superlinear convergence rate of these quasi-Newton methods has been extensively studied, but their explicit finite time local convergence rate has not been established yet. In this paper, we provide a finite time (non-asymptotic) convergence analysis for BFGS and DFP methods under the assumptions that the objective function is strongly convex, its gradient is Lipschitz continuous, and its Hessian is Lipschitz continuous only in the direction of the optimal solution. We show that in a local neighborhood of the optimal solution, the iterates generated by both DFP and BFGS converge to the optimal solution at a superlinear rate of $\mathcal{O}((\frac{1}{ {k}})^{k/2})$, where $k$ is the number of iterations. In particular, for a specific choice of the local neighborhood, both DFP and BFGS converge to the optimal solution at the rate of $(\frac{0.85}{k})^{k/2}$. Our theoretical guarantee is one of the first results that provide a non-asymptotic superlinear convergence rate for DFP and BFGS quasi-Newton methods.