Non-asymptotic Superlinear Convergence of Standard Quasi-Newton Methods

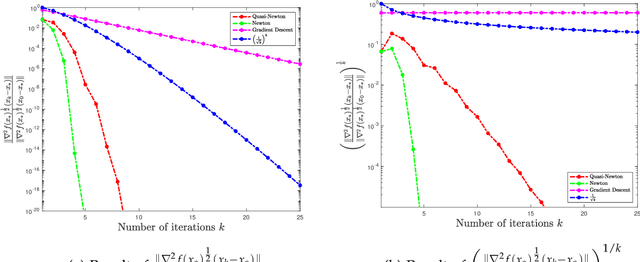
In this paper, we study the non-asymptotic superlinear convergence rate of DFP and BFGS, which are two well-known quasi-Newton methods. The asymptotic superlinear convergence rate of these quasi-Newton methods has been extensively studied, but their explicit finite time local convergence rate has not been established yet. In this paper, we provide a finite time (non-asymptotic) convergence analysis for BFGS and DFP methods under the assumptions that the objective function is strongly convex, its gradient is Lipschitz continuous, and its Hessian is Lipschitz continuous only in the direction of the optimal solution. We show that in a local neighborhood of the optimal solution, the iterates generated by both DFP and BFGS converge to the optimal solution at a superlinear rate of $\mathcal{O}((\frac{1}{ {k}})^{k/2})$, where $k$ is the number of iterations. In particular, for a specific choice of the local neighborhood, both DFP and BFGS converge to the optimal solution at the rate of $(\frac{0.85}{k})^{k/2}$. Our theoretical guarantee is one of the first results that provide a non-asymptotic superlinear convergence rate for DFP and BFGS quasi-Newton methods.