Yunsong Zhang
Design, Dynamic Modeling and Control of a 2-DOF Robotic Wrist Actuated by Twisted and Coiled Actuators
Mar 07, 2025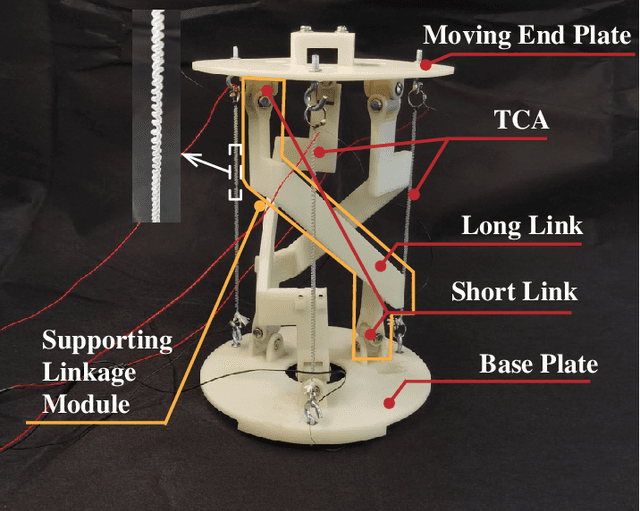
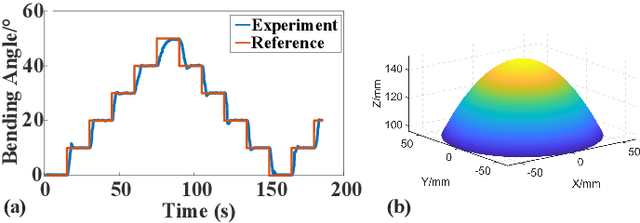
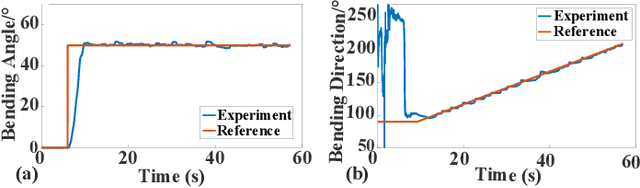
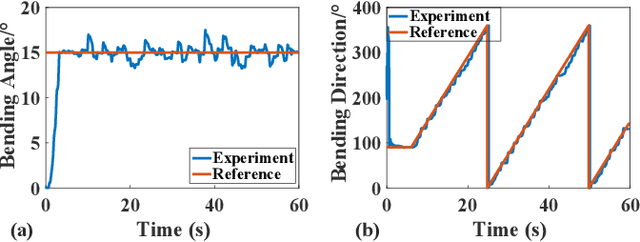
Abstract:Robotic wrists play a pivotal role in the functionality of industrial manipulators and humanoid robots, facilitating manipulation and grasping tasks. In recent years, there has been a growing interest in integrating artificial muscle-driven actuators for robotic wrists, driven by advancements in technology offering high energy density, lightweight construction, and compact designs. However, in the study of robotic wrists driven by artificial muscles, dynamic model-based controllers are often overlooked, despite their critical importance for motion analysis and dynamic control of robots. This paper presents a novel design of a two-degree-of-freedom (2-DOF) robotic wrist driven by twisted and coiled actuators (TCA) utilizing a parallel mechanism with a 3RRRR configuration. The proposed robotic wrist is expected to feature lightweight structures and superior motion performance while mitigating friction issues. The Lagrangian dynamic model of the wrist is established, along with a nonlinear model predictive controller (NMPC) designed for trajectory tracking tasks. A prototype of the robotic wrist is developed, and extensive experiments are conducted to validate its superior motion performance and the proposed dynamic model. Subsequently, extensive comparative experiments between NMPC and PID controller were conducted under various operating conditions. The experimental results demonstrate the effectiveness and robustness of the dynamic model-based controller in the motion control of TCA-driven robotic wrists.
An Efficient Learning Control Framework With Sim-to-Real for String-Type Artificial Muscle-Driven Robotic Systems
May 17, 2024



Abstract:Robotic systems driven by artificial muscles present unique challenges due to the nonlinear dynamics of actuators and the complex designs of mechanical structures. Traditional model-based controllers often struggle to achieve desired control performance in such systems. Deep reinforcement learning (DRL), a trending machine learning technique widely adopted in robot control, offers a promising alternative. However, integrating DRL into these robotic systems faces significant challenges, including the requirement for large amounts of training data and the inevitable sim-to-real gap when deployed to real-world robots. This paper proposes an efficient reinforcement learning control framework with sim-to-real transfer to address these challenges. Bootstrap and augmentation enhancements are designed to improve the data efficiency of baseline DRL algorithms, while a sim-to-real transfer technique, namely randomization of muscle dynamics, is adopted to bridge the gap between simulation and real-world deployment. Extensive experiments and ablation studies are conducted utilizing two string-type artificial muscle-driven robotic systems including a two degree-of-freedom robotic eye and a parallel robotic wrist, the results of which demonstrate the effectiveness of the proposed learning control strategy.
A Federated Learning Framework for Nonconvex-PL Minimax Problems
May 29, 2021
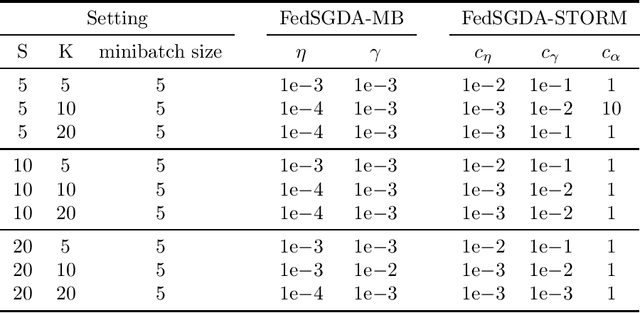
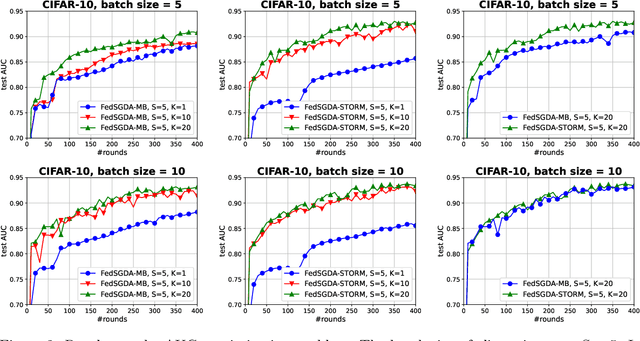
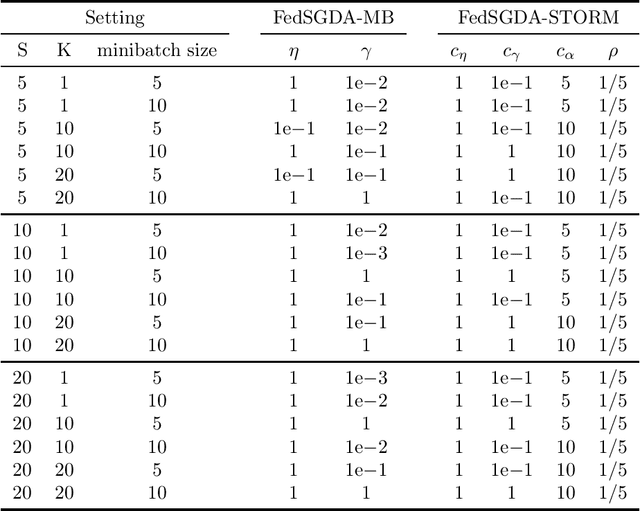
Abstract:We consider a general class of nonconvex-PL minimax problems in the cross-device federated learning setting. Although nonconvex-PL minimax problems have received a lot of interest in recent years, existing algorithms do not apply to the cross-device federated learning setting which is substantially different from conventional distributed settings and poses new challenges. To bridge this gap, we propose an algorithmic framework named FedSGDA. FedSGDA performs multiple local update steps on a subset of active clients in each round and leverages global gradient estimates to correct the bias in local update directions. By incorporating FedSGDA with two representative global gradient estimators, we obtain two specific algorithms. We establish convergence rates of the proposed algorithms by using novel potential functions. Experimental results on synthetic and real data corroborate our theory and demonstrate the effectiveness of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge