Learning in games from a stochastic approximation viewpoint
Paper and Code
Jun 08, 2022
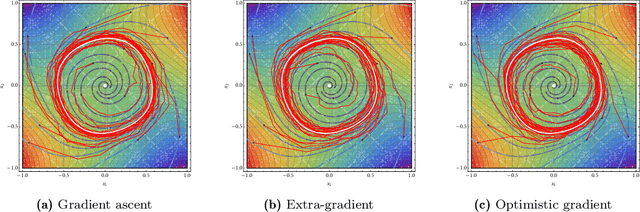
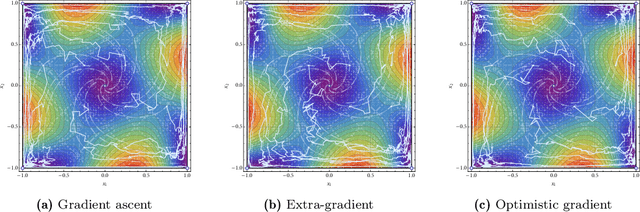
We develop a unified stochastic approximation framework for analyzing the long-run behavior of multi-agent online learning in games. Our framework is based on a "primal-dual", mirrored Robbins-Monro (MRM) template which encompasses a wide array of popular game-theoretic learning algorithms (gradient methods, their optimistic variants, the EXP3 algorithm for learning with payoff-based feedback in finite games, etc.). In addition to providing an integrated view of these algorithms, the proposed MRM blueprint allows us to obtain a broad range of new convergence results, both asymptotic and in finite time, in both continuous and finite games.
* 39 pages, 6 figures, 1 table
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge