Recovering Stochastic Dynamics via Gaussian Schrödinger Bridges

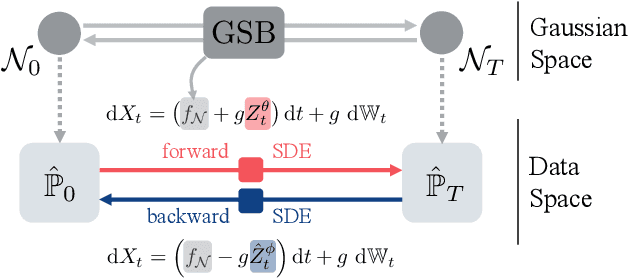
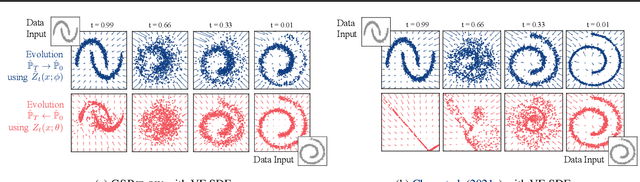
We propose a new framework to reconstruct a stochastic process $\left\{\mathbb{P}_{t}: t \in[0, T]\right\}$ using only samples from its marginal distributions, observed at start and end times $0$ and $T$. This reconstruction is useful to infer population dynamics, a crucial challenge, e.g., when modeling the time-evolution of cell populations from single-cell sequencing data. Our general framework encompasses the more specific Schr\"odinger bridge (SB) problem, where $\mathbb{P}_{t}$ represents the evolution of a thermodynamic system at almost equilibrium. Estimating such bridges is notoriously difficult, motivating our proposal for a novel adaptive scheme called the GSBflow. Our goal is to rely on Gaussian approximations of the data to provide the reference stochastic process needed to estimate SB. To that end, we solve the \acs{SB} problem with Gaussian marginals, for which we provide, as a central contribution, a closed-form solution and SDE-representation. We use these formulas to define the reference process used to estimate more complex SBs, and show that this does indeed help with its numerical solution. We obtain notable improvements when reconstructing both synthetic processes and single-cell genomics experiments.