PolarGrad: A Class of Matrix-Gradient Optimizers from a Unifying Preconditioning Perspective

The ever-growing scale of deep learning models and datasets underscores the critical importance of efficient optimization methods. While preconditioned gradient methods such as Adam and AdamW are the de facto optimizers for training neural networks and large language models, structure-aware preconditioned optimizers like Shampoo and Muon, which utilize the matrix structure of gradients, have demonstrated promising evidence of faster convergence. In this paper, we introduce a unifying framework for analyzing "matrix-aware" preconditioned methods, which not only sheds light on the effectiveness of Muon and related optimizers but also leads to a class of new structure-aware preconditioned methods. A key contribution of this framework is its precise distinction between preconditioning strategies that treat neural network weights as vectors (addressing curvature anisotropy) versus those that consider their matrix structure (addressing gradient anisotropy). This perspective provides new insights into several empirical phenomena in language model pre-training, including Adam's training instabilities, Muon's accelerated convergence, and the necessity of learning rate warmup for Adam. Building upon this framework, we introduce PolarGrad, a new class of preconditioned optimization methods based on the polar decomposition of matrix-valued gradients. As a special instance, PolarGrad includes Muon with updates scaled by the nuclear norm of the gradients. We provide numerical implementations of these methods, leveraging efficient numerical polar decomposition algorithms for enhanced convergence. Our extensive evaluations across diverse matrix optimization problems and language model pre-training tasks demonstrate that PolarGrad outperforms both Adam and Muon.

Adaptive Batch Size Schedules for Distributed Training of Language Models with Data and Model Parallelism

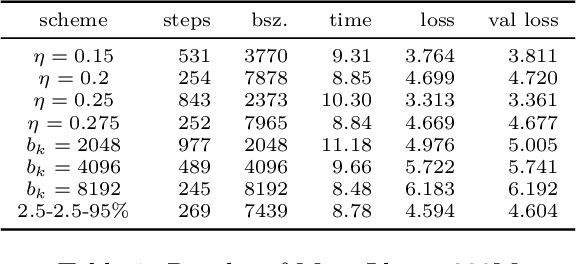
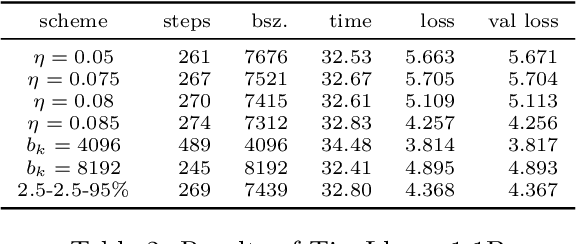
An appropriate choice of batch sizes in large-scale model training is crucial, yet it involves an intrinsic yet inevitable dilemma: large-batch training improves training efficiency in terms of memory utilization, while generalization performance often deteriorates due to small amounts of gradient noise. Despite this dilemma, the common practice of choosing batch sizes in language model training often prioritizes training efficiency -- employing either constant large sizes with data parallelism or implementing batch size warmup schedules. However, such batch size schedule designs remain heuristic and often fail to adapt to training dynamics, presenting the challenge of designing adaptive batch size schedules. Given the abundance of available datasets and the data-hungry nature of language models, data parallelism has become an indispensable distributed training paradigm, enabling the use of larger batch sizes for gradient computation. However, vanilla data parallelism requires replicas of model parameters, gradients, and optimizer states at each worker, which prohibits training larger models with billions of parameters. To optimize memory usage, more advanced parallelism strategies must be employed. In this work, we propose general-purpose and theoretically principled adaptive batch size schedules compatible with data parallelism and model parallelism. We develop a practical implementation with PyTorch Fully Sharded Data Parallel, facilitating the pretraining of language models of different sizes. We empirically demonstrate that our proposed approaches outperform constant batch sizes and heuristic batch size warmup schedules in the pretraining of models in the Llama family, with particular focus on smaller models with up to 3 billion parameters. We also establish theoretical convergence guarantees for such adaptive batch size schedules with Adam for general smooth nonconvex objectives.

Communication-Efficient Adaptive Batch Size Strategies for Distributed Local Gradient Methods

Modern deep neural networks often require distributed training with many workers due to their large size. As worker numbers increase, communication overheads become the main bottleneck in data-parallel minibatch stochastic gradient methods with per-iteration gradient synchronization. Local gradient methods like Local SGD reduce communication by only syncing after several local steps. Despite understanding their convergence in i.i.d. and heterogeneous settings and knowing the importance of batch sizes for efficiency and generalization, optimal local batch sizes are difficult to determine. We introduce adaptive batch size strategies for local gradient methods that increase batch sizes adaptively to reduce minibatch gradient variance. We provide convergence guarantees under homogeneous data conditions and support our claims with image classification experiments, demonstrating the effectiveness of our strategies in training and generalization.

AdAdaGrad: Adaptive Batch Size Schemes for Adaptive Gradient Methods

The choice of batch sizes in stochastic gradient optimizers is critical for model training. However, the practice of varying batch sizes throughout the training process is less explored compared to other hyperparameters. We investigate adaptive batch size strategies derived from adaptive sampling methods, traditionally applied only in stochastic gradient descent. Given the significant interplay between learning rates and batch sizes, and considering the prevalence of adaptive gradient methods in deep learning, we emphasize the need for adaptive batch size strategies in these contexts. We introduce AdAdaGrad and its scalar variant AdAdaGradNorm, which incrementally increase batch sizes during training, while model updates are performed using AdaGrad and AdaGradNorm. We prove that AdaGradNorm converges with high probability at a rate of $\mathscr{O}(1/K)$ for finding a first-order stationary point of smooth nonconvex functions within $K$ iterations. AdaGrad also demonstrates similar convergence properties when integrated with a novel coordinate-wise variant of our adaptive batch size strategies. Our theoretical claims are supported by numerical experiments on various image classification tasks, highlighting the enhanced adaptability of progressive batching protocols in deep learning and the potential of such adaptive batch size strategies with adaptive gradient optimizers in large-scale model training.

Non-Log-Concave and Nonsmooth Sampling via Langevin Monte Carlo Algorithms

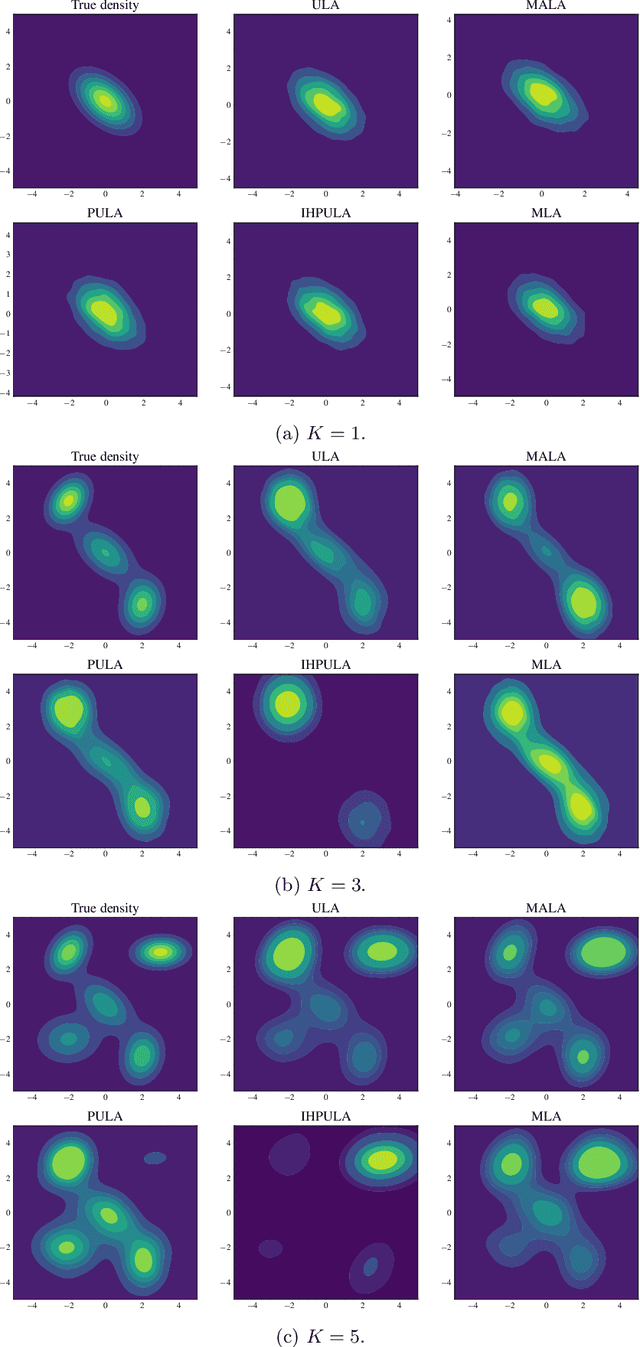
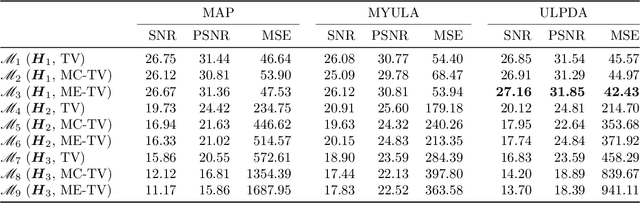
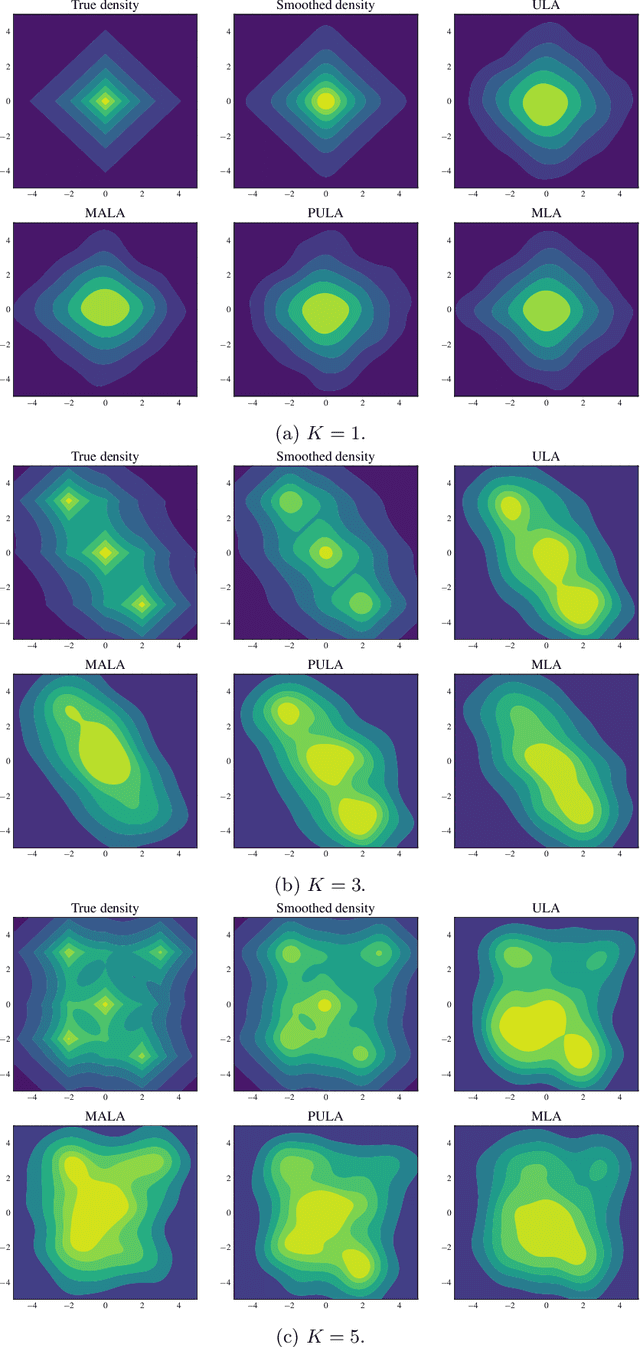
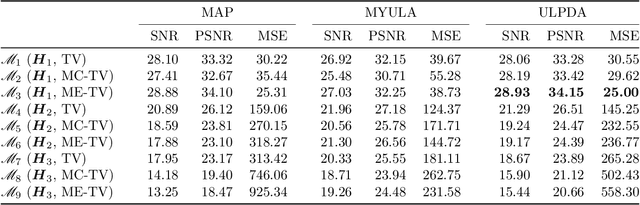
We study the problem of approximate sampling from non-log-concave distributions, e.g., Gaussian mixtures, which is often challenging even in low dimensions due to their multimodality. We focus on performing this task via Markov chain Monte Carlo (MCMC) methods derived from discretizations of the overdamped Langevin diffusions, which are commonly known as Langevin Monte Carlo algorithms. Furthermore, we are also interested in two nonsmooth cases for which a large class of proximal MCMC methods have been developed: (i) a nonsmooth prior is considered with a Gaussian mixture likelihood; (ii) a Laplacian mixture distribution. Such nonsmooth and non-log-concave sampling tasks arise from a wide range of applications to Bayesian inference and imaging inverse problems such as image deconvolution. We perform numerical simulations to compare the performance of most commonly used Langevin Monte Carlo algorithms.

Bregman Proximal Langevin Monte Carlo via Bregman--Moreau Envelopes

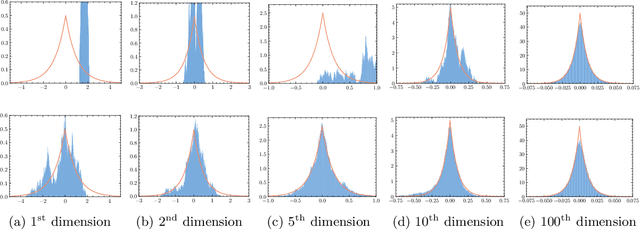
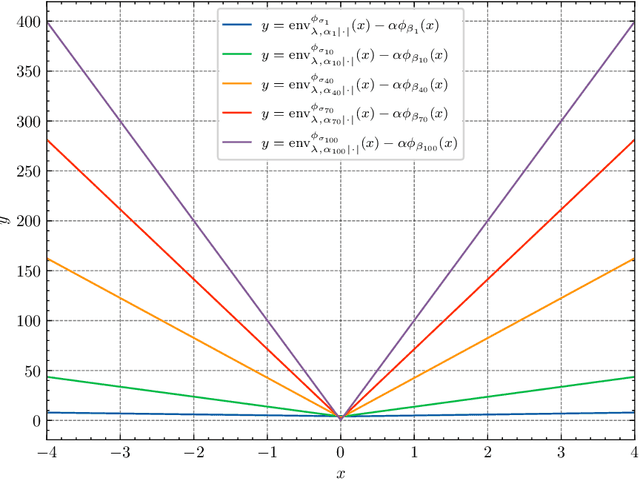
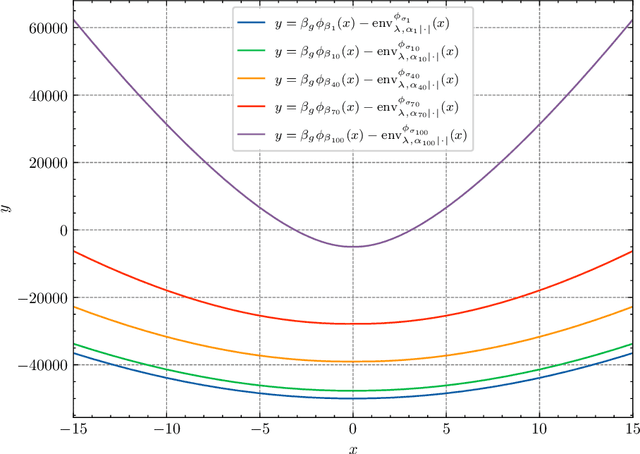
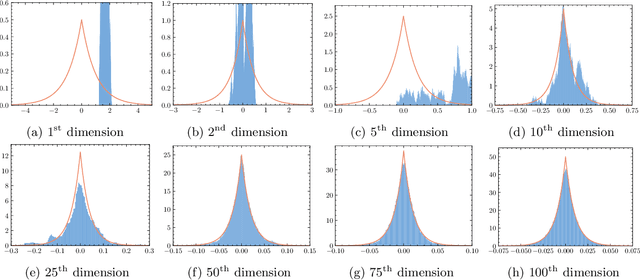
We propose efficient Langevin Monte Carlo algorithms for sampling distributions with nonsmooth convex composite potentials, which is the sum of a continuously differentiable function and a possibly nonsmooth function. We devise such algorithms leveraging recent advances in convex analysis and optimization methods involving Bregman divergences, namely the Bregman--Moreau envelopes and the Bregman proximity operators, and in the Langevin Monte Carlo algorithms reminiscent of mirror descent. The proposed algorithms extend existing Langevin Monte Carlo algorithms in two aspects -- the ability to sample nonsmooth distributions with mirror descent-like algorithms, and the use of the more general Bregman--Moreau envelope in place of the Moreau envelope as a smooth approximation of the nonsmooth part of the potential. A particular case of the proposed scheme is reminiscent of the Bregman proximal gradient algorithm. The efficiency of the proposed methodology is illustrated with various sampling tasks at which existing Langevin Monte Carlo methods are known to perform poorly.

Wasserstein Distributionally Robust Optimization via Wasserstein Barycenters

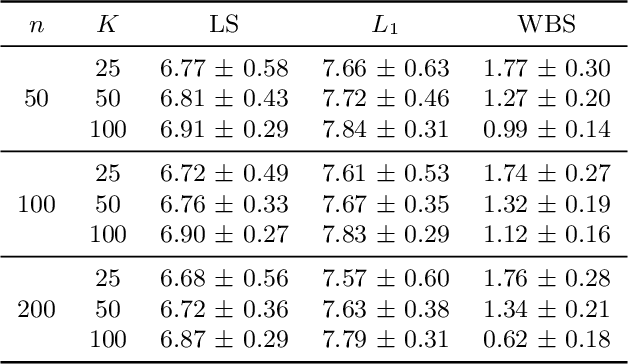
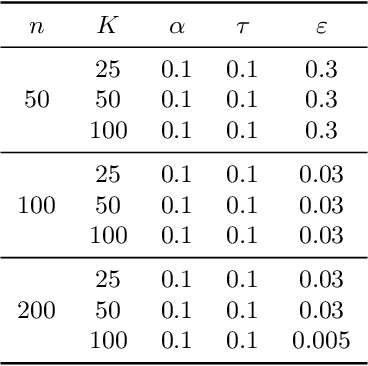
In many applications in statistics and machine learning, the availability of data samples from multiple sources has become increasingly prevalent. On the other hand, in distributionally robust optimization, we seek data-driven decisions which perform well under the most adverse distribution from a nominal distribution constructed from data samples within a certain distance of probability distributions. However, it remains unclear how to achieve such distributional robustness when data samples from multiple sources are available. In this paper, we propose constructing the nominal distribution in Wasserstein distributionally robust optimization problems through the notion of Wasserstein barycenter as an aggregation of data samples from multiple sources. Under specific choices of the loss function, the proposed formulation admits a tractable reformulation as a finite convex program, with powerful finite-sample and asymptotic guarantees. We illustrate our proposed method through concrete examples with nominal distributions of location-scatter families and distributionally robust maximum likelihood estimation.

The Multi-Agent Pickup and Delivery Problem: MAPF, MARL and Its Warehouse Applications

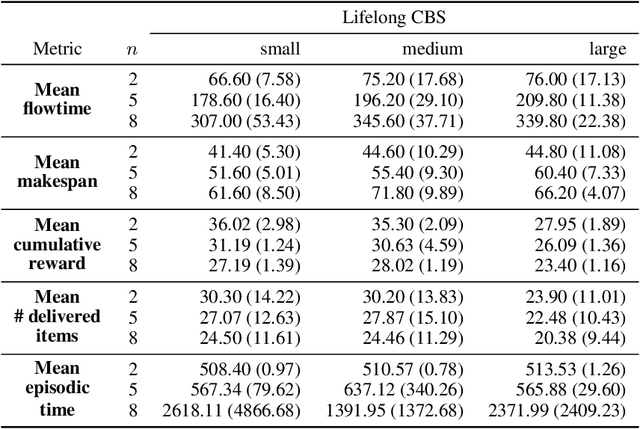
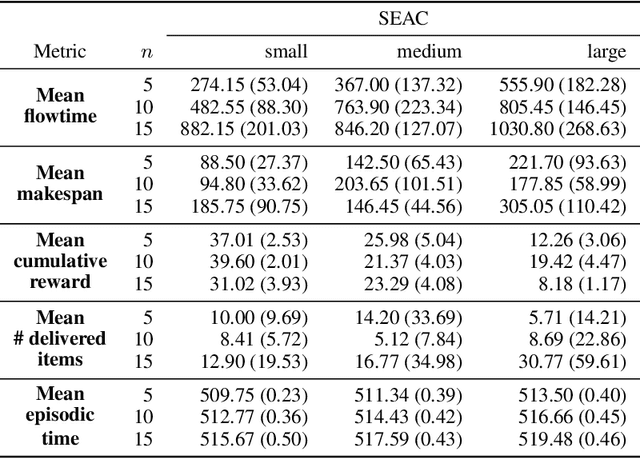
We study two state-of-the-art solutions to the multi-agent pickup and delivery (MAPD) problem based on different principles -- multi-agent path-finding (MAPF) and multi-agent reinforcement learning (MARL). Specifically, a recent MAPF algorithm called conflict-based search (CBS) and a current MARL algorithm called shared experience actor-critic (SEAC) are studied. While the performance of these algorithms is measured using quite different metrics in their separate lines of work, we aim to benchmark these two methods comprehensively in a simulated warehouse automation environment.

Global Convergence in Deep Learning with Variable Splitting via the Kurdyka-Łojasiewicz Property

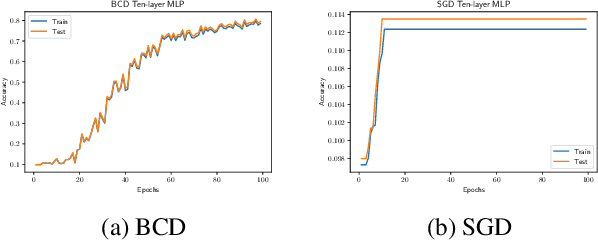
Deep learning has recently attracted a significant amount of attention due to its great empirical success. However, the effectiveness in training deep neural networks (DNN) remains a mystery in the associated nonconvex optimizations. In this paper, we aim to provide some theoretical understanding on such optimization problems. In particular, the Kurdyka-{\L}ojasiewicz (KL) property is established for DNN training with variable splitting schemes, which leads to the global convergence of block coordinate descent (BCD) type algorithms to a critical point of objective functions under natural conditions of DNN. Some existing BCD algorithms can be viewed as special cases in this framework. Experiments further show that the proposed algorithms may find network parameters of approximately zero training loss (error) with over-parameterized models.

A Proximal Block Coordinate Descent Algorithm for Deep Neural Network Training

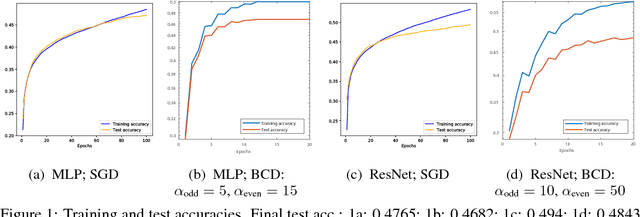
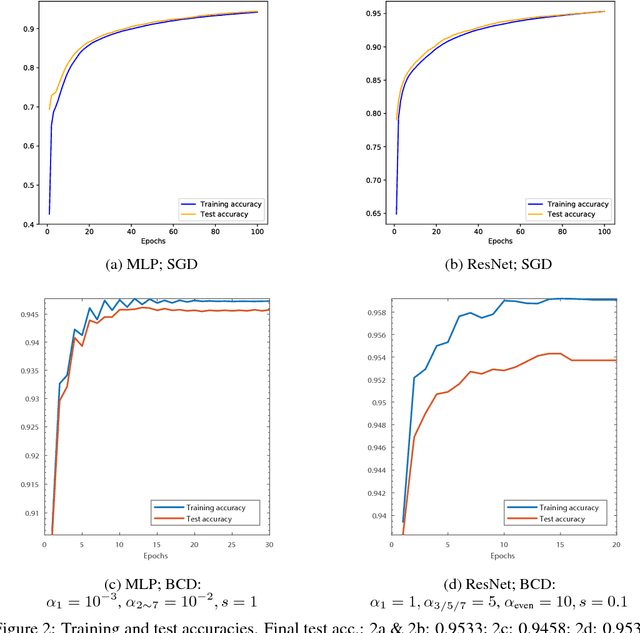
Training deep neural networks (DNNs) efficiently is a challenge due to the associated highly nonconvex optimization. The backpropagation (backprop) algorithm has long been the most widely used algorithm for gradient computation of parameters of DNNs and is used along with gradient descent-type algorithms for this optimization task. Recent work have shown the efficiency of block coordinate descent (BCD) type methods empirically for training DNNs. In view of this, we propose a novel algorithm based on the BCD method for training DNNs and provide its global convergence results built upon the powerful framework of the Kurdyka-Lojasiewicz (KL) property. Numerical experiments on standard datasets demonstrate its competitive efficiency against standard optimizers with backprop.