Global Convergence in Deep Learning with Variable Splitting via the Kurdyka-Łojasiewicz Property
Paper and Code
Jun 11, 2018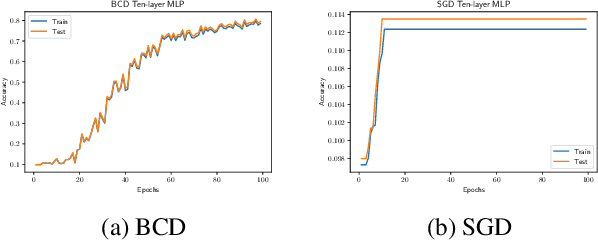
Deep learning has recently attracted a significant amount of attention due to its great empirical success. However, the effectiveness in training deep neural networks (DNN) remains a mystery in the associated nonconvex optimizations. In this paper, we aim to provide some theoretical understanding on such optimization problems. In particular, the Kurdyka-{\L}ojasiewicz (KL) property is established for DNN training with variable splitting schemes, which leads to the global convergence of block coordinate descent (BCD) type algorithms to a critical point of objective functions under natural conditions of DNN. Some existing BCD algorithms can be viewed as special cases in this framework. Experiments further show that the proposed algorithms may find network parameters of approximately zero training loss (error) with over-parameterized models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge