Explore the Power of Synthetic Data on Few-shot Object Detection

Few-shot object detection (FSOD) aims to expand an object detector for novel categories given only a few instances for training. The few training samples restrict the performance of FSOD model. Recent text-to-image generation models have shown promising results in generating high-quality images. How applicable these synthetic images are for FSOD tasks remains under-explored. This work extensively studies how synthetic images generated from state-of-the-art text-to-image generators benefit FSOD tasks. We focus on two perspectives: (1) How to use synthetic data for FSOD? (2) How to find representative samples from the large-scale synthetic dataset? We design a copy-paste-based pipeline for using synthetic data. Specifically, saliency object detection is applied to the original generated image, and the minimum enclosing box is used for cropping the main object based on the saliency map. After that, the cropped object is randomly pasted on the image, which comes from the base dataset. We also study the influence of the input text of text-to-image generator and the number of synthetic images used. To construct a representative synthetic training dataset, we maximize the diversity of the selected images via a sample-based and cluster-based method. However, the severe problem of high false positives (FP) ratio of novel categories in FSOD can not be solved by using synthetic data. We propose integrating CLIP, a zero-shot recognition model, into the FSOD pipeline, which can filter 90% of FP by defining a threshold for the similarity score between the detected object and the text of the predicted category. Extensive experiments on PASCAL VOC and MS COCO validate the effectiveness of our method, in which performance gain is up to 21.9% compared to the few-shot baseline.

An Effective Crop-Paste Pipeline for Few-shot Object Detection

Few-shot object detection (FSOD) aims to expand an object detector for novel categories given only a few instances for training. However, detecting novel categories with only a few samples usually leads to the problem of misclassification. In FSOD, we notice the false positive (FP) of novel categories is prominent, in which the base categories are often recognized as novel ones. To address this issue, a novel data augmentation pipeline that Crops the Novel instances and Pastes them on the selected Base images, called CNPB, is proposed. There are two key questions to be answered: (1) How to select useful base images? and (2) How to combine novel and base data? We design a multi-step selection strategy to find useful base data. Specifically, we first discover the base images which contain the FP of novel categories and select a certain amount of samples from them for the base and novel categories balance. Then the bad cases, such as the base images that have unlabeled ground truth or easily confused base instances, are removed by using CLIP. Finally, the same category strategy is adopted, in which a novel instance with category n is pasted on the base image with the FP of n. During combination, a novel instance is cropped and randomly down-sized, and thus pasted at the assigned optimal location from the randomly generated candidates in a selected base image. Our method is simple yet effective and can be easy to plug into existing FSOD methods, demonstrating significant potential for use. Extensive experiments on PASCAL VOC and MS COCO validate the effectiveness of our method.

Explore the Power of Dropout on Few-shot Learning

The generalization power of the pre-trained model is the key for few-shot deep learning. Dropout is a regularization technique used in traditional deep learning methods. In this paper, we explore the power of dropout on few-shot learning and provide some insights about how to use it. Extensive experiments on the few-shot object detection and few-shot image classification datasets, i.e., Pascal VOC, MS COCO, CUB, and mini-ImageNet, validate the effectiveness of our method.

A Unified Framework with Meta-dropout for Few-shot Learning

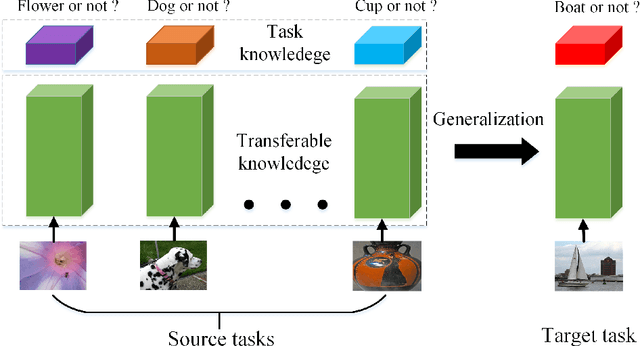
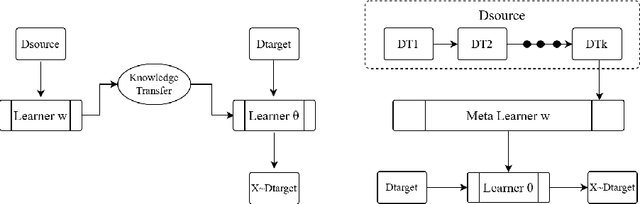
Conventional training of deep neural networks usually requires a substantial amount of data with expensive human annotations. In this paper, we utilize the idea of meta-learning to explain two very different streams of few-shot learning, i.e., the episodic meta-learning-based and pre-train finetune-based few-shot learning, and form a unified meta-learning framework. In order to improve the generalization power of our framework, we propose a simple yet effective strategy named meta-dropout, which is applied to the transferable knowledge generalized from base categories to novel categories. The proposed strategy can effectively prevent neural units from co-adapting excessively in the meta-training stage. Extensive experiments on the few-shot object detection and few-shot image classification datasets, i.e., Pascal VOC, MS COCO, CUB, and mini-ImageNet, validate the effectiveness of our method.

Learning through deterministic assignment of hidden parameters

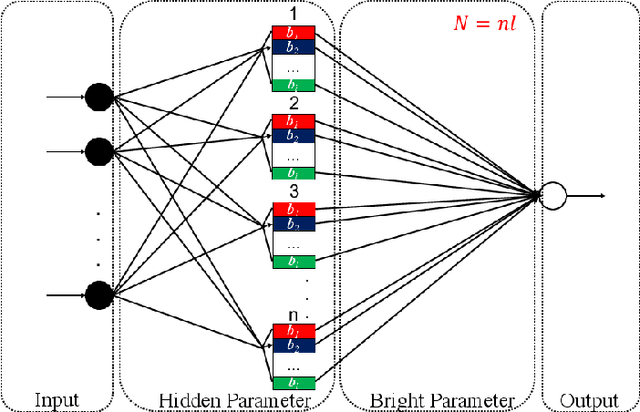
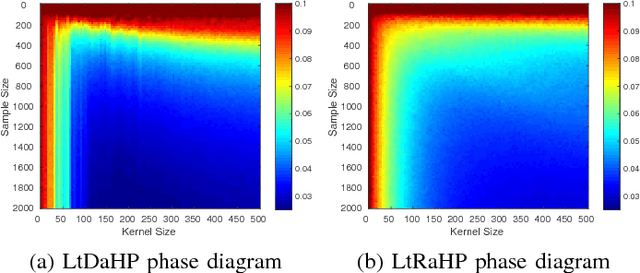
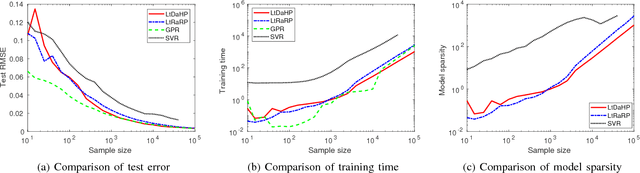
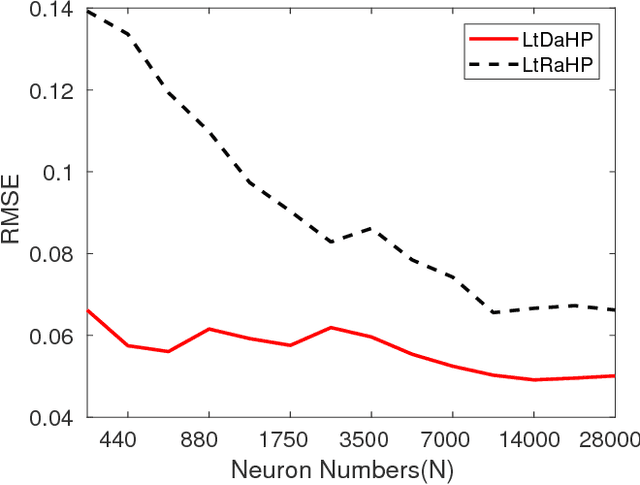
Supervised learning frequently boils down to determining hidden and bright parameters in a parameterized hypothesis space based on finite input-output samples. The hidden parameters determine the attributions of hidden predictors or the nonlinear mechanism of an estimator, while the bright parameters characterize how hidden predictors are linearly combined or the linear mechanism. In traditional learning paradigm, hidden and bright parameters are not distinguished and trained simultaneously in one learning process. Such an one-stage learning (OSL) brings a benefit of theoretical analysis but suffers from the high computational burden. To overcome this difficulty, a two-stage learning (TSL) scheme, featured by learning through deterministic assignment of hidden parameters (LtDaHP) was proposed, which suggests to deterministically generate the hidden parameters by using minimal Riesz energy points on a sphere and equally spaced points in an interval. We theoretically show that with such deterministic assignment of hidden parameters, LtDaHP with a neural network realization almost shares the same generalization performance with that of OSL. We also present a series of simulations and application examples to support the outperformance of LtDaHP

Global Convergence in Deep Learning with Variable Splitting via the Kurdyka-Łojasiewicz Property

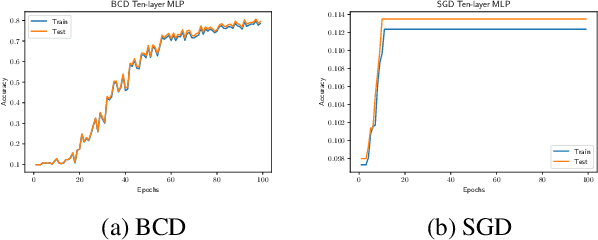
Deep learning has recently attracted a significant amount of attention due to its great empirical success. However, the effectiveness in training deep neural networks (DNN) remains a mystery in the associated nonconvex optimizations. In this paper, we aim to provide some theoretical understanding on such optimization problems. In particular, the Kurdyka-{\L}ojasiewicz (KL) property is established for DNN training with variable splitting schemes, which leads to the global convergence of block coordinate descent (BCD) type algorithms to a critical point of objective functions under natural conditions of DNN. Some existing BCD algorithms can be viewed as special cases in this framework. Experiments further show that the proposed algorithms may find network parameters of approximately zero training loss (error) with over-parameterized models.

Constructive neural network learning

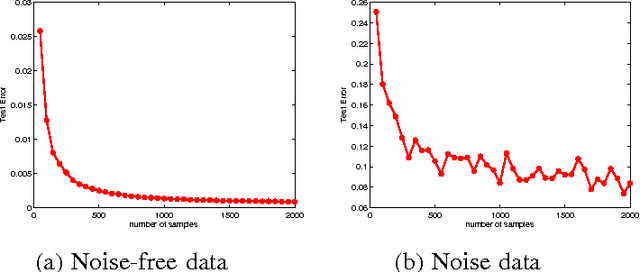
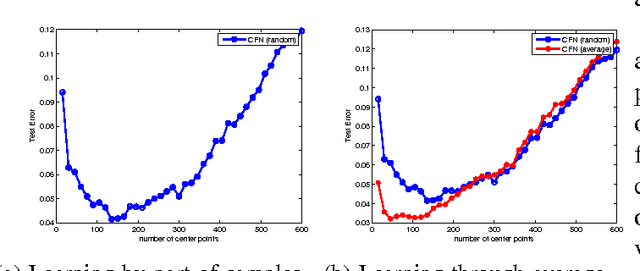
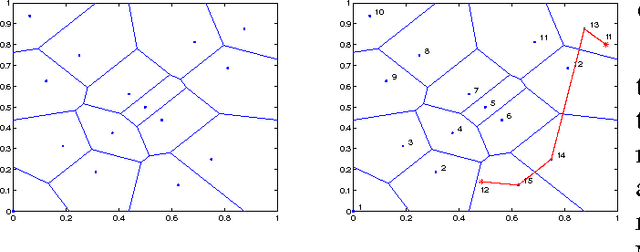
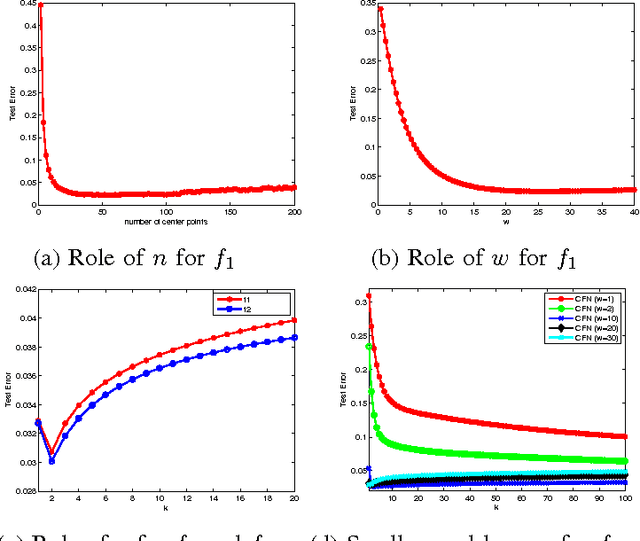
In this paper, we aim at developing scalable neural network-type learning systems. Motivated by the idea of "constructive neural networks" in approximation theory, we focus on "constructing" rather than "training" feed-forward neural networks (FNNs) for learning, and propose a novel FNNs learning system called the constructive feed-forward neural network (CFN). Theoretically, we prove that the proposed method not only overcomes the classical saturation problem for FNN approximation, but also reaches the optimal learning rate when the regression function is smooth, while the state-of-the-art learning rates established for traditional FNNs are only near optimal (up to a logarithmic factor). A series of numerical simulations are provided to show the efficiency and feasibility of CFN via comparing with the well-known regularized least squares (RLS) with Gaussian kernel and extreme learning machine (ELM).

Greedy Criterion in Orthogonal Greedy Learning

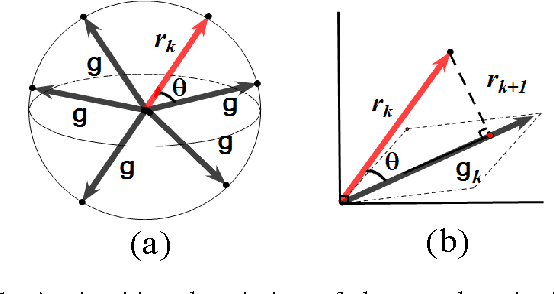
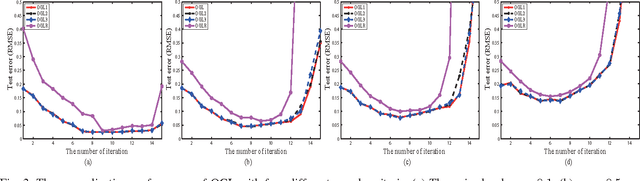
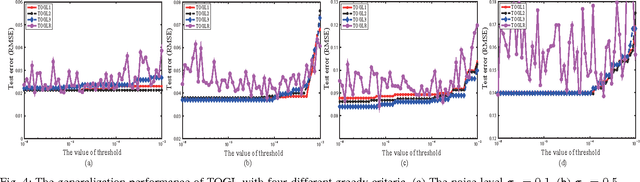
Orthogonal greedy learning (OGL) is a stepwise learning scheme that starts with selecting a new atom from a specified dictionary via the steepest gradient descent (SGD) and then builds the estimator through orthogonal projection. In this paper, we find that SGD is not the unique greedy criterion and introduce a new greedy criterion, called "$\delta$-greedy threshold" for learning. Based on the new greedy criterion, we derive an adaptive termination rule for OGL. Our theoretical study shows that the new learning scheme can achieve the existing (almost) optimal learning rate of OGL. Plenty of numerical experiments are provided to support that the new scheme can achieve almost optimal generalization performance, while requiring less computation than OGL.

Divide and Conquer Local Average Regression

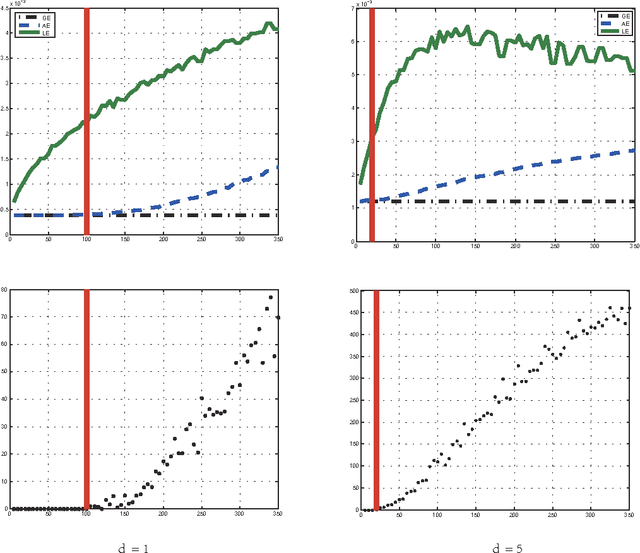
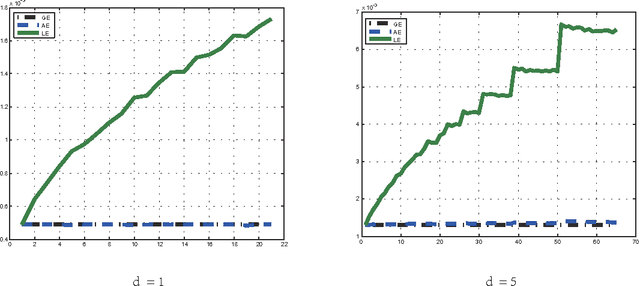
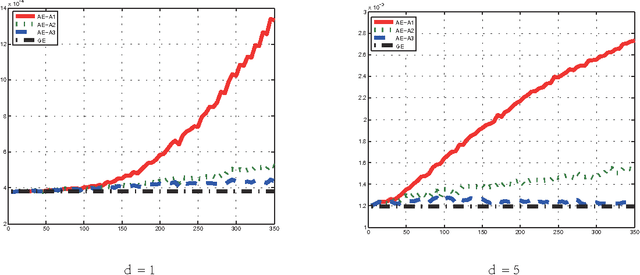
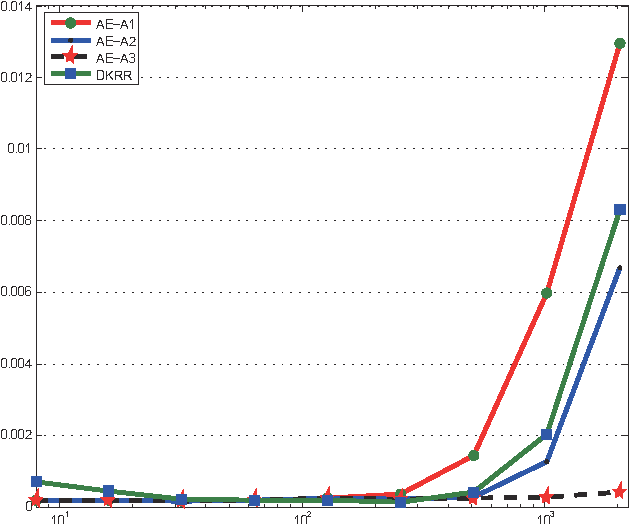
The divide and conquer strategy, which breaks a massive data set into a se- ries of manageable data blocks, and then combines the independent results of data blocks to obtain a final decision, has been recognized as a state-of-the-art method to overcome challenges of massive data analysis. In this paper, we merge the divide and conquer strategy with local average regression methods to infer the regressive relationship of input-output pairs from a massive data set. After theoretically analyzing the pros and cons, we find that although the divide and conquer local average regression can reach the optimal learning rate, the restric- tion to the number of data blocks is a bit strong, which makes it only feasible for small number of data blocks. We then propose two variants to lessen (or remove) this restriction. Our results show that these variants can achieve the optimal learning rate with much milder restriction (or without such restriction). Extensive experimental studies are carried out to verify our theoretical assertions.

Nonparametric regression using needlet kernels for spherical data

Needlets have been recognized as state-of-the-art tools to tackle spherical data, due to their excellent localization properties in both spacial and frequency domains. This paper considers developing kernel methods associated with the needlet kernel for nonparametric regression problems whose predictor variables are defined on a sphere. Due to the localization property in the frequency domain, we prove that the regularization parameter of the kernel ridge regression associated with the needlet kernel can decrease arbitrarily fast. A natural consequence is that the regularization term for the kernel ridge regression is not necessary in the sense of rate optimality. Based on the excellent localization property in the spacial domain further, we also prove that all the $l^{q}$ $(01\leq q < \infty)$ kernel regularization estimates associated with the needlet kernel, including the kernel lasso estimate and the kernel bridge estimate, possess almost the same generalization capability for a large range of regularization parameters in the sense of rate optimality. This finding tentatively reveals that, if the needlet kernel is utilized, then the choice of $q$ might not have a strong impact in terms of the generalization capability in some modeling contexts. From this perspective, $q$ can be arbitrarily specified, or specified merely by other no generalization criteria like smoothness, computational complexity, sparsity, etc..