Constructive neural network learning
Paper and Code
Apr 30, 2016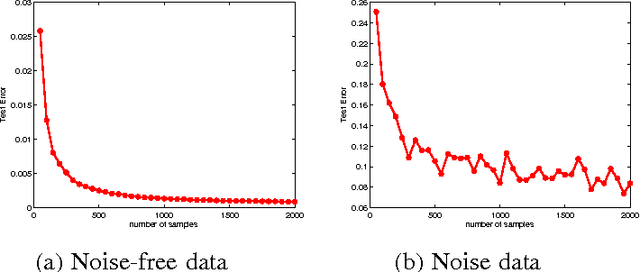
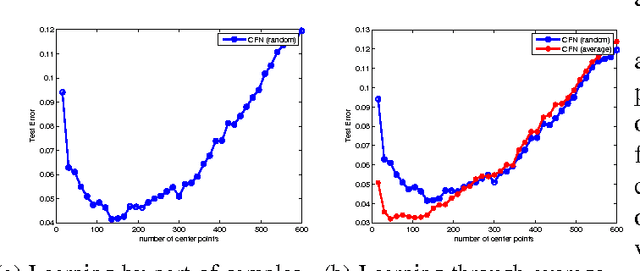
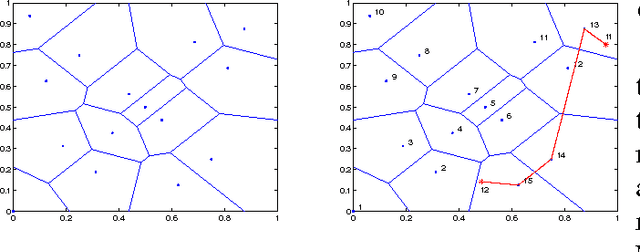
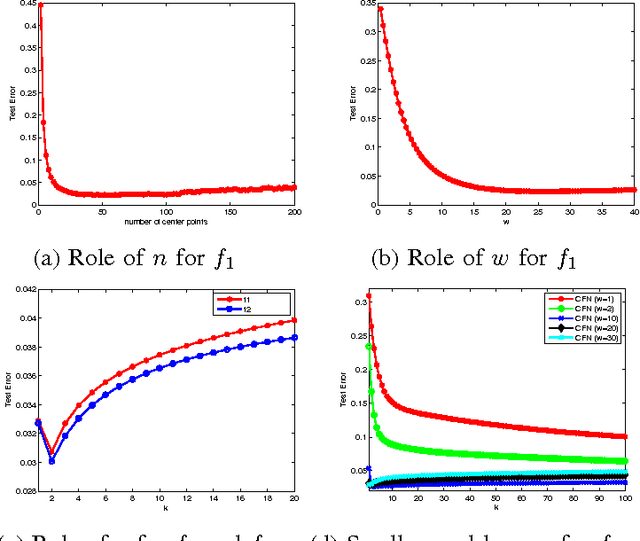
In this paper, we aim at developing scalable neural network-type learning systems. Motivated by the idea of "constructive neural networks" in approximation theory, we focus on "constructing" rather than "training" feed-forward neural networks (FNNs) for learning, and propose a novel FNNs learning system called the constructive feed-forward neural network (CFN). Theoretically, we prove that the proposed method not only overcomes the classical saturation problem for FNN approximation, but also reaches the optimal learning rate when the regression function is smooth, while the state-of-the-art learning rates established for traditional FNNs are only near optimal (up to a logarithmic factor). A series of numerical simulations are provided to show the efficiency and feasibility of CFN via comparing with the well-known regularized least squares (RLS) with Gaussian kernel and extreme learning machine (ELM).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge